Coordenadas polares y cartesianas
Para indicar dónde estás en un mapa o gráfico hay dos sistemas:
Coordenadas cartesianas
Con coordenadas cartesianas señalas un punto diciendo la distancia de lado y la distancia vertical:
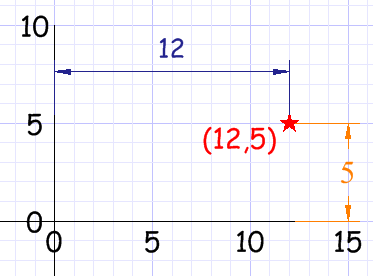
Coordenadas polares
Con coordenadas polares señalas un punto diciendo la distancia y el ángulo que se forma:
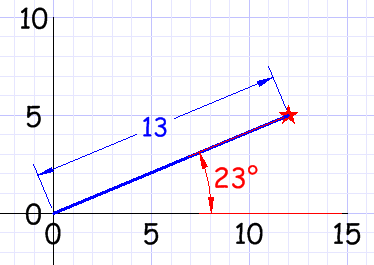
Convertir
Para convertir de un sistema a otro, se resuelve el triángulo:
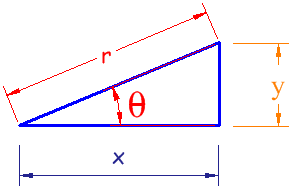
De cartesianas a polares
Si tienes un punto en coordenadas cartesianas (x,y) y lo quieres en coordenadas polares (r,θ), necesitas resolver un triángulo del que conoces dos lados.
Ejemplo: ¿qué es (12,5) en coordenadas polares?
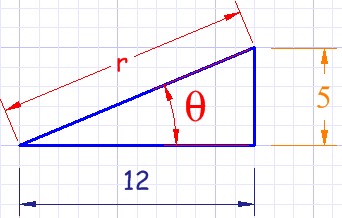
Usamos el teorema de Pitágoras para calcular el lado largo (la hipotenusa):
r2 = 122 + 52
r = √ (122 + 52)
r = √ (144 + 25) = √ (169) = 13
Usa la función tangente para calcular el ángulo:
tan( θ ) = 5 / 12
θ = atan( 5 / 12 ) = 22.6°
Así que las fórmulas para convertir coordenadas cartesianas (x,y) a polares (r,θ) son:
r = √ (x2 + y2)
θ = atan( y / x )
De polares a cartesianas
Si tienes un punto en coordenadas polares (r, θ) y lo quieres en coordenadas cartesianas (x,y) necesitas resolver un triángulo del que conoces el lado largo y un ángulo:
Ejemplo: ¿qué es (13, 23 °) en coordenadas cartesianas?
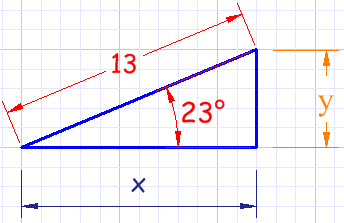
| Usamos la función coseno para x: | cos( 23 °) = x / 13 |
| Cambiamos de orden y resolvemos: | x = 13 × cos( 23 °) = 13 × 0.921 = 11.98 |
| Usamos la función seno para y: | sin( 23 °) = y / 13 |
| Cambiamos de orden y resolvemos: | y = 13 × sin( 23 °) = 13 × 0.391 = 5.08 |
Así que las fórmulas para convertir coordenadas polares (r,θ) a cartesianas (x,y) son:
x = r × cos( θ )
y = r × sin( θ )
¡Y ya está!

