Polinomios: Regla de los Signos
Una forma especial de saber cuántas raíces positivas y negativas tiene un polinomio.
Un Polinomio tiene esta forma:
| un ejemplo de polinomio este tiene 3 términos |
Los polinomios tienen "raíces" (ceros), donde son iguales a 0:
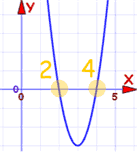
Las raíces están en x=2 y x=4
Tiene 2 raíces, ambas son positivas (+2 y +4)
A veces no sabemos dónde están las raíces, pero podemos decir cuántas son positivas o negativas....
... solo contando cuántas veces cambia
el signo
(de más a menos, o de menos a más)
Déjame mostrarte con un ejemplo:
Ejemplo: 4x + x2 − 3x5 − 2
¿Cuántas de las raíces son positivas?
Primero, reescribe el polinomio del exponente más alto al más bajo (ignora cualquier término "cero", por lo que en este ejemplo no importa que x4 y x3 no estén):
−3x5 + x2 + 4x − 2
Luego, cuenta cuántas veces hay un cambio de signo (de más a menos, o de menos a más):
El número de cambios de signo es el número máximo de raíces positivas.
Hay 2 cambios en el signo, por lo que hay como máximo 2 raíces positivas (quizás menos).
Entonces, ¿podría haber 2, 1 o 0 raíces positivas?
Pero en realidad no habrá solo 1 raíz positiva ... sigue leyendo ...
Raíces complejas
También puede haber raíces complejas.
Un Número Complejo es la combinación de un Número Real y un Número Imaginario
Pero...
¡Las raíces complejas siempre vienen en pares!
¿Siempre en parejas? Sí. Entonces obtenemos:
- no hay raíces complejas,
- 2 raíces complejas,
- 4 raíces complejas,
- etc.
El número de raíces positivas
Tener raíces complejas reducirá el número de raíces positivas en 2 (o en 4, ó 6, ... etc.), en otras palabras, en un número par.Entonces, en nuestro ejemplo anterior, en lugar de 2 raíces positivas, podría haber 0 raíces positivas:
El número de raíces positivas es 2 o 0
Esta es la regla general:
El número de raíces positivas es igual al número de cambios de signo, o un valor menor que ese por un múltiplo de 2
Ejemplo: si el número máximo de raíces positivas era 5, entonces podría haber 5, o 3 o 1 raíces positivas.
¿Cuántas de las raíces son negativas?
Al hacer un cálculo similar, podemos descubrir cuántas raíces son negativas ...
... pero primero necesitamos poner "−x" en lugar de "x", así:
Y luego tenemos que resolver los signos:
- −3(−x)5 se convierte en +3x5
- +(−x)2 se convierte en +x2 (no hay cambio de signo)
- +4(−x) se convierte en −4x
Así que tenemos:
+3x5 + x2 − 4x − 2
El truco es que solo los exponentes impares, como 1, 3, 5, etc., revertirán su signo.
Ahora solo contamos los cambios como antes:
Un solo cambio, por lo que hay 1 raíz
negativa.
¡Pero recuerda reducirlo porque puede haber raíces complejas!
Pero espera ... solo podemos reducirlo en un número par ... y 1 no puede reducirse más ... así que 1 raíz negativa es la única opción.
Número total de raíces
En la página Teorema Fundamental del Álgebra explicamos que un polinomio tendrá exactamente tantas raíces como su grado (el grado es el máximo exponente del polinomio).
Entonces sabemos una cosa más: el grado es 5, por lo que hay
5 raíces en total.
Lo que sabemos hasta ahora
OK, hemos reunido mucha información. Sabemos todo esto:
- raíces positivas: 2 o 0
- raíces negativas: 1
- número total de raíces: 5
Entonces, después de pensarlo un poco, el resultado general es:
- 5 raíces: 2 positivas, 1 negativa, 2 complejas (un par), o
- 5 raíces: 0 positivas, 1 negativa, 4 complejas (dos pares)
¡Y logramos resolver todo eso solo con base en los signos y exponentes!
Debe tener un término constante
Un último punto importante:
Antes de usar la Regla de signos, el polinomio debe tener un término constante (como "+2" o "−5")
Si no es así, entonces factoriza x hasta que lo tenga.
Ejemplo: 2x4 + 3x2 − 4x
¡No hay término constante! Así que factoriza"x":
x(2x3 + 3x − 4)
Esto significa que x=0 es una de las raíces.Ahora haga la "Regla de Signos" para:
2x3 + 3x − 4
Cuenta los cambios de signos para raíces positivas:
Solo hay un cambio de signo,
Entonces hay 1 raíz positiva
Y el caso negativo (después de cambiar los signos de exponentes de valores impares):
No hay cambios de signos,
Entonces no hay raíces negativas
El grado es 3, por lo que esperamos 3 raíces. Solo hay una combinación posible:
- 3 raíces: 1 positiva, 0 negativas y 2 complejas
Y ahora, volviendo a la pregunta original:
2x4 + 3x2 − 4x
Tendrá:
- 4 raíces: 1 cero, 1 positiva, 0 negativas y 2 complejas
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota:
están en inglés).
Nota histórica: La regla de los signos fue descrita por primera vez por René Descartes en 1637, y a veces se la llama la Regla de los Signos de Descartes.

