Teorema Fundamental del Álgebra
El "Teorema Fundamental del Álgebra" no es el comienzo del álgebra ni nada, pero sí dice algo interesante sobre polinomios:
Cualquier polinomio de grado n
tiene n raíces
pero es posible que necesitemos usar números complejos
Permíteme explicar:
Un Polinomio se ve así:
| ejemplo de un polinomio este tiene 3 términos |
Una "raíz" (o "cero") es donde el polinomio es igual a cero.
Entonces, un polinomio de grado 3 tendrá 3 raíces (lugares donde el polinomio es igual a cero). Un polinomio de grado 4 tendrá 4 raíces. Y así.
Ejemplo: ¿cuáles son las raíces de x2 − 9?
x2 − 9 tiene grado 2 (el mayor exponente de x es
2), por lo que hay 2 raíces.
Vamos a resolverlo. Queremos que sea igual a cero:
Suma 9 de ambos lados:
Luego toma la raíz cuadrada de ambos lados:
Así que las raíces son −3 y +3
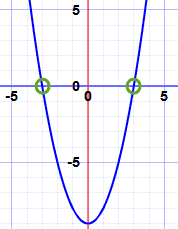
Y hay algo más de interés:
Un polinomio se puede reescribir así:
Ejemplo: x2 − 9
Las raíces son r1 = −3 y r2 = +3 (como descubrimos anteriormente), entonces los factores son:
(en este caso, a es igual a 1, así que no lo puse)
Los Factores Lineales son (x+3) y (x−3)
Aquí hay otro ejemplo:
Ejemplo: 3x2 − 12
Es de grado 2, por lo que hay 2 raíces.Encontremos las raíces: queremos que sea igual a cero:
3 y 12 tienen un factor común de 3:
Podemos resolver x2 − 4 si movemos el −4 al lado derecho y sacamos la raíz cuadrada:
Por lo tanto, las raíces son:
x = −2 y x = +2
Y entonces los factores son:
3x2 − 12 = 3(x+2)(x−2)
Del mismo modo, cuando conocemos los factores de un polinomio, también conocemos las raíces.
Ejemplo: 3x2 − 18x + 24
Es de grado 2, por lo que hay 2 factores.
3x2 − 18x + 24 = a(x−r1)(x−r2)
Casualmente sé que esta es la factorización:
3x2 − 18x + 24 = 3(x−2)(x−4)
Y entonces las raíces (ceros) son:
- +2
- +4
Veamos esas raíces:
3(2)2 − 18(2) + 24 = 12 − 36 + 24 = 0
3(4)2 − 18(4) + 24 = 48 − 72 + 24 = 0
¡Sí! El polinomio es cero en x = +2 y x = +4
Números complejos
Es posible que necesitemos usar números complejos para hacer que el polinomio sea igual a cero.
Un Número Complejo es una combinación de un Número Real y un Número Imaginario
Y aquí hay un ejemplo:
Ejemplo: x2−x+1
¿Podemos hacer que sea igual a cero?
x2−x+1 = 0
Usando el Solucionador de Ecuaciones Cuadráticas la respuesta (a 3 decimales) es:
| 0.5 − 0.866i | y | 0.5 + 0.866i |
¡Son números complejos! Pero también funcionan.
Y entonces los factores son:
x2 − x + 1 = ( x − (0.5−0.866i ) )( x − (0.5+0.866i ) )
Pares complejos
De modo que las raíces r1, r2, ... etc. pueden ser Números Reales o Complejos.
Pero hay algo interesante ...
¡Las raíces complejas siempre vienen en pares!
Lo viste en nuestro ejemplo anterior:
Ejemplo: x2−x+1
Tiene las raíces:
| 0.5 − 0.866i | y | 0.5 + 0.866i |
El par en realidad son conjugados complejos (donde cambiamos el signo del medio) como este:
Entonces obtenemos:
- 0 raíces complejas
- 2 raíces complejas
- 4 raíces complejas,
- etc.
Lo que significa que automáticamente sabemos esto:
| Grado | Raíces | Combinaciones Posibles |
|---|---|---|
| 1 | 1 | 1 raíz real |
| 2 | 2 | 2 raíces reales, o 2 raíces complejas |
| 3 | 3 | 3 raíces reales, o 1 raíz real y 2 raíces complejas |
| 4 | 4 | 4 raíces reales, o 2 raíces reales y 2 raíces complejas , o 4 raíces complejas |
| etc. | etc! |
De modo que:
Cuando el grado es impar (1, 3, 5, etc.) hay al menos una raíz real ... ¡garantizado!
Ejemplo: 3x−6
El grado es 1.
Hay una raíz real
Está en +2:
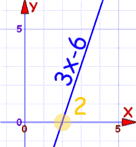 :
:
De hecho, puedes ver que debe pasar por el eje x en algún momento.
¡Pero lo real también es complejo!
He estado diciendo "Real" y "Complejo", pero los Números Complejos ya incluyen los Números Reales.
Entonces, cuando digo que hay "2 raíces reales y 2 raíces complejas", debería decir algo como "2 raíces puramente reales (sin parte imaginaria) y 2 raíces complejas (con una parte imaginaria distinta de cero)" ...
... pero esas son muchas palabras que suenan confusas ...
... así que espero que no te importe mi (quizás demasiado) lenguaje simple.
¿No quieres números complejos?
Si no queremos números complejos, podemos multiplicar pares de raíces complejas:
(a + bi)(a − bi) = a2 + b2
Se obtiene una Ecuación Cuadrática sin Números Complejos ... es puramente Real.
Ese tipo de cuadrática (donde no podemos "reducirla" más sin usar números complejos) se llama cuadrática irreducible.
Y recuerda que los factores simples como (x−r1) se llaman Factores Lineales.
Por lo tanto, un polinomio se puede factorizar en todos los valores reales usando:
- Factores Lineales, y
- Cuadráticas Irreducibles
Ejemplo: x3−1
x3−1 = (x−1)(x2+x+1)
Se ha factorizado en:
- 1 factor lineal: (x−1)
- 1 factor cuadrático irreducible: (x2+x+1)
Para factorizar (x2+x+1) más necesitamos usar números complejos, por lo que es una "cuadrática irreducible".
¿Cómo sabemos si la cuadrática es irreducible?
Simplemente calculamos el "discriminante": b2 - 4ac
(Lee Ecuaciones Cuadráticas para aprender más sobre el discriminante.)
Cuando b2 − 4ac es
negativo, la cuadrática tiene soluciones complejas,
y por lo tanto es "irreducible"
Ejemplo: 2x2+3x+5
a = 2, b = 3, y c = 5:
b2 − 4ac = 32 − 4×2×5 = 9−40 = −31
El discriminante es negativo, por lo que es un "Cuadrático Irreducible".
Multiplicidad
A veces aparece un factor más de una vez. Esa es su multiplicidad.
Ejemplo: x2−6x+9
x2−6x+9 = (x−3)(x−3)
"(x−3)" aparece dos veces, entonces la raíz "3" tiene Multiplicidad 2
Las Multiplicidades se incluyen cuando decimos "un polinomio de grado n tiene n raíces".
Ejemplo: x4+x3
Debe haber 4 raíces (y 4 factores), ¿verdad?
Factorizarla es sencillo, solo saca el x3:
x4+x3 = x3(x+1) = x·x·x·(x+1)
Hay 4 factores, con "x" apareciendo 3 veces.
Pero parece haber solo 2 raíces, en x=−1 y x=0:
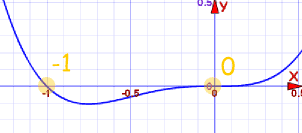
Pero contando Multiplicidades, en realidad hay 4:
- "x" aparece tres veces, por lo que la raíz "0" tiene Multiplicidad 3
- "x+1" aparece una vez, por lo que la raíz "−1" tiene Multiplicidad 1
Total = 3+1 = 4
Resumen
- Un polinomio de grado n tiene n raíces (donde el polinomio es cero)
- Un polinomio se puede factorizar como: a(x−r1)(x−r2)... donde r1, etc. son las raíces
- Las raíces pueden necesitar ser números complejos
- Las raíces complejas siempre vienen en pares
- Multiplicar un par de factores complejos da una cuadrática irreducible
- Por lo tanto, un polinomio se puede factorizar en todos los factores reales que son:
- Factores lineales o
- Cuadráticos irreducibles
- A veces aparece un factor más de una vez. Esa es su multiplicidad.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).



