Hallar Máximos y Mínimos Usando Derivadas
¿En qué punto una función tiene un punto alto o bajo? ¡El cálculo puede ayudar!
Un máximo es un punto alto y un mínimo es un punto bajo:
En una función que cambia suavemente, un máximo o mínimo se encuentra
siempre donde la función se aplana (excepto en un punto silla).
¿Dónde se aplana? Donde la
pendiente es cero.
¿Dónde la pendiente es igual a cero? ¡La derivada nos lo dice!
Vamos a explorar un ejemplo:
Ejemplo: se lanza una pelota al aire. Su altura en cualquier instante t viene dada por:
h = 3 + 14t − 5t2
¿Cuál es su altura máxima?
Al hacer uso de las derivadas podemos encontrar la pendiente de esa función:
h' = 0 + 14 − 5(2t)
= 14 − 10t
(Mira a continuación este ejemplo para ver cómo encontramos esa derivada).
Ahora encuentra en dónde la pendiente es cero:
La pendiente es cero en t = 1.4 segundos
Y la altura en ese momento es:
Finalmente:
La altura máxima es 12.8 m (en t = 1.4 s)
Un repaso rápido sobre derivadas
Podría decirse que una derivada
básicamente encuentra la pendiente de una función.
En el ejemplo anterior tomamos:
h = 3 + 14t − 5t2
y obtuvimos esta derivada:
h' = 0 + 14 − 5(2t)
= 14 − 10t
La cual nos dice la pendiente de la función en cualquier instante t
Usamos estas Reglas de Derivación:
- La pendiente de un valor constante (como 3) es 0
- La pendiente de una línea como 2x es 2, por lo que 14t tiene una pendiente de 14
- Una función cuadrada como t2 tiene una pendiente de 2t, por lo que 5t2 tiene una pendiente de 5(2t)
- Y luego sumamos todo: 0 + 14 − 5(2t)
¿Cómo sabemos que es un máximo (o mínimo)?
¡Lo vemos en la gráfica! Pero de lo contrario ... las derivadas
vuelven al rescate.
Toma la derivada de la pendiente (es decir, la segunda
derivada de la función original):
La Derivada de 14 − 10t es −10
Esto significa que la pendiente se hace cada vez más pequeña (−10): viajando de izquierda a derecha, la pendiente comienza en positivo (la función aumenta), pasa por cero (el punto plano) y luego la pendiente se vuelve negativa (la función disminuye):
Una pendiente que se hace más pequeña (y pasa por 0) significa un
máximo.
A esto se le llama la Prueba de la Segunda Derivada
En el gráfico de arriba mostré la pendiente antes y después, pero en la práctica hacemos la prueba en el punto donde la pendiente es cero:
Prueba de la Segunda Derivada
Cuando se tiene una función cuya pendiente es cero en x, y la segunda derivada en x es:
- menor que 0, entonces es un máximo local
- mayor que 0, entonces es un mínimo local
- igual a 0, la prueba falla (puede haber otras formas de averiguarlo)
Ejemplo: Encuentra los máximos y mínimos para:
y = 5x3 + 2x2 − 3x
La derivada (pendiente) es:
y' = 15x2 + 4x − 3
La cual es cuadrática con ceros en:
- x = −3/5
- x = +1/3
¿Podrían ser máximos o mínimos? (¡No mires la gráfica todavía!)
La segunda derivada es y'' = 30x + 4
En x = −3/5:
En x = +1/3:
(Ahora puedes mirar la gráfica).
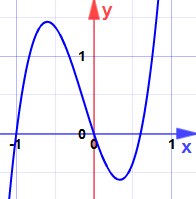
Glosario
Decimos máximo (o mínimo) local cuando puede haber puntos más altos (o más bajos) en otro lugar pero no cerca.
Otro ejemplo
Ejemplo: Encuentra los máximos y mínimos para:
y = x3 − 6x2 + 12x − 5
La derivada es:
y' = 3x2 − 12x + 12
La cual es cuadrática con un solo cero en x = 2
¿Es un máximo o un mínimo?
La segunda derivada es y'' = 6x − 12
En x = 2:
Y esta es la razón:
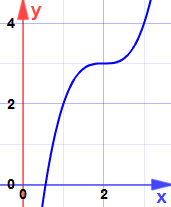
Es un punto silla ... la pendiente se vuelve cero, pero no es ni máxima ni mínima.
Debe ser diferenciable
Hay una cuestión técnica importante:
La función debe ser diferenciable
(la derivada debe existir en cada punto de su dominio).
Ejemplo: ¿Qué tal la función f(x) = |x| (valor absoluto) ?
| |x| se ve así: |  |
¡En x=0 tiene un cambio muy puntiagudo!
De hecho, no es diferenciable allí (como se muestra en la página
sobre diferenciabilidad).
Entonces no podemos usar este método para la función de valor absoluto.
La función también debe ser continua, pero cualquier función diferenciable también es continua, por lo que no hay necesidad de preocuparse por eso.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
