Funciones Hiperbólicas

Las dos funciones hiperbólicas básicas son "sinh" y "cosh":

Seno hiperbólico:

sinh(x) = e^x − e^−x 2

Coseno hiperbólico:

cosh(x) = e^x + e^−x 2

 

Estas funciones usan la función exponencial natural e^x

Y no son lo mismo que sin (x) y cos (x), pero tienen un poco de similitud:

sinh vs sin

cosh vs cos

Catenaria

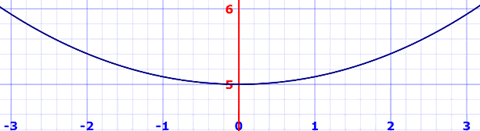
Uno de los usos interesantes de las funciones hiperbólicas es la curva que forman los cables o cadenas suspendidos.

Un cable colgante forma una curva denominada catenaria definida mediante la función cosh:

f(x) = a cosh(x/a)

Como en este ejemplo de la página longitud de arco:

Otras funciones hiperbólicas

De sinh y cosh podemos crear:

Tangente hiperbólica "tanh":

tanh(x) = sinh(x) cosh(x) = e^x − e^−x e^x + e^−x

tanh vs tan

 

Cotangente hiperbólica:

coth(x) = cosh(x) sinh(x) = e^x + e^−x e^x − e^−x

 

Secante hiperbólica:

sech(x) = 1 cosh(x) = 2 e^x + e^−x

 

Cosecante hiperbólica: "csch" o "cosech":

csch(x) = 1 sinh(x) = 2 e^x − e^−x

¿Por qué la palabra "hiperbólica"?

Porque proviene de mediciones realizadas en una hipérbola:

Entonces, al igual que las funciones trigonométricas se relacionan con un círculo, las funciones hiperbólicas se relacionan con una hipérbola.

Identidades

• sinh(−x) = −sinh(x)
• cosh(−x) = cosh(x)

Y también:

• tanh(−x) = −tanh(x)
• coth(−x) = −coth(x)
• sech(−x) = sech(x)
• csch(−x) = −csch(x)

Par e impar

Tanto cosh como sech son funciones pares, el resto son funciones impares.

Derivadas

Sus derivadas son:

d dx sinh(x) = cosh(x)

d dx cosh(x) = sinh(x)

d dx tanh(x) = 1 − tanh²(x)