Ejemplos en el Mundo Real de Ecuaciones Cuadráticas

Una Ecuación Cuadrática se ve así:

Ecuación Cuadrática

Las Ecuaciones Cuadráticas aparecen en muchas situaciones del mundo real!

Aquí hemos recopilado algunos ejemplos para ti, y resolvemos cada uno usando diferentes métodos:

Cada ejemplo sigue tres etapas generales:

Toma la descripción del mundo real y elabora algunas ecuaciones.
¡Resuelve!
Usa tu sentido común para interpretar los resultados

lanzamiento de pelota

Pelotas, Flechas, Misiles y Piedras

Cuando lanzas una pelota (o disparas una flecha, disparas un misil o lanzas una piedra), se eleva en el aire, disminuyendo la rapidez a medida que sube, y luego desciende cada vez más rápido ...

... !Y una Ecuación Cuadrática te dice su posición en todo momento!

Ejemplo: lanzar una pelota

Se lanza una pelota hacia arriba, desde 3m sobre el suelo, con una velocidad de 14 m/s. ¿Cuándo toca el suelo?

Ignorando la resistencia del aire, podemos calcular su altura sumando estas tres cosas:
(Nota: t es el tiempo en segundos)

La altura comienza a 3m:		3
Viaja hacia arriba a 14 metros por segundo (14 m/s):		14t
La gravedad lo empuja hacia abajo, cambiando su posición aproximadamente 5m por segundo al cuadrado:		−5t²
(Nota para los lectores ávidos: el -5t² surge de simplificar -(½)at² con a=9.8 m/s²)

Súmalos y se tiene que la altura h en cualquier momento t es:

h = 3 + 14t − 5t²

Y la pelota golpeará el suelo cuando la altura sea cero:

3 + 14t − 5t² = 0

¡Y esto es una Ecuación Cuadrática!

En "Forma Estándar" se ve así:

−5t² + 14t + 3 = 0

Se ve aún mejor cuando multiplicamos todos los términos por −1:

5t² − 14t − 3 = 0

Vamos a resolverla...

Hay muchas maneras de resolverla, aquí la factorizaremos usando el método "Encuentra dos números que se multiplican para dar a×c, y que sumados dan b" que se explica en Factorizando Cuadráticas:

a×c = −15, y b = −14.

Los factores de −15 son: −15, −5, −3, −1, 1, 3, 5, 15

Al probar algunas combinaciones, encontramos que −15 y 1 funcionan (−15×1 = −15, y −15+1 = −14)

Reescribe lo de en medio con −15 y 1:5t² − 15t + t − 3 = 0

Factoriza los primeros dos y los últimos dos:5t(t − 3) + 1(t − 3) = 0

El factor común es (t − 3):(5t + 1)(t − 3) = 0

Y las dos soluciones son:5t + 1 = 0 o t − 3 = 0

t = −0.2 o t = 3

"t = −0.2" es un tiempo negativo, imposible en nuestro caso.

Entonces "t = 3" es la respuesta que queremos:

¡La pelota toca el suelo después de 3 segundos!

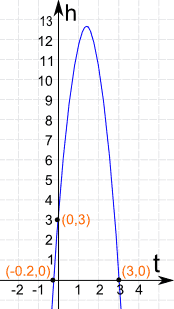
gráfica cuadrática de la pelota

Aquí está la gráfica de la Parábola h = −5t² + 14t + 3

Te muestra la altura de la pelota frente al tiempo.

Algunos puntos interesantes:

(0,3) Cuando t = 0 (al inicio) la pelota está a 3 m

(−0.2,0) dice que −0.2 segundos ANTES de tirar la pelota estaba a nivel del suelo. ¡Esto nunca sucedió! Entonces nuestro sentido común dice ignorarlo.

(3,0) dice que a los 3 segundos la pelota está al nivel del suelo.

Observa también que la pelota alcanza casi 13 metros de altura.

Nota: ¡Puedes encontrar exactamente dónde está el punto superior!

El método se explica en Graficando Ecuaciones Cuadráticas, y tiene dos pasos:

Encuentra dónde (a lo largo del eje horizontal) se produce el punto superior usando −b/2a:

t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 segundos

Luego encuentra la altura usando ese valor (1.4)

h = −5t² + 14t + 3 = −5(1.4)² + 14 × 1.4 + 3 = 12.8 metros

Entonces la pelota alcanza el punto más alto de 12.8 metros después de 1.4 segundos.

Ejemplo: nueva bicicleta deportiva

¡Has diseñado un nuevo estilo de bicicleta deportiva!

Ahora deseas hacer muchas de ellas y venderlas con fines de lucro.

Tus costos serán:

$700,000 para costes de la instalación, publicidad, etc.
$110 para hacer cada bicicleta

curva de demanda de ventas de bicicletas

Basado en bicicletas similares, puedes esperar que las ventas sigan esta "curva de demanda":

Unidades vendidas = 70,000 − 200P

Donde "P" es el precio.

Por ejemplo, si estableces el precio:

a $ 0, simplemente regalas 70,000 bicicletas
a $ 350, no venderás ninguna bicicleta
a $ 300 puedes vender 70,000 - 200 × 300 = 10,000 bicicletas

Entonces ... ¿cuál es el mejor precio? ¿Y cuántas deberías fabricar?

¡Hagamos algunas ecuaciones!

La cantidad que vendas depende del precio, así que usa "P" para el precio como variable

Unidades vendidas = 70,000 − 200P
Ventas en dólares = Unidades × Precio = (70,000 − 200P) × P = 70,000P − 200P²
Costos = 700,000 + 110 × (70,000 − 200P) = 700,000 + 7,700,000 − 22,000P = 8,400,000 − 22,000P
Ganancia = Ventas − Costos = 70,000P - 200P² − (8,400,000 − 22,000P) = −200P² + 92,000P − 8,400,000

Ganancia = −200P² + 92,000P − 8,400,000

Sí, una ecuación cuadrática. Vamos a resolverla Completando el Cuadrado.

Resolver: −200P² + 92,000P − 8,400,000 = 0

Paso 1 Divide los términos entre -200

P² – 460P + 42000 = 0

Paso 2 Mueve el término constante al lado derecho de la ecuación:

P² – 460P = −42000

Paso 3 Completa el cuadrado en el lado izquierdo de la ecuación y equilibra esto sumando el mismo número al lado derecho de la ecuación:

(b/2)² = (−460/2)² = (−230)² = 52900

P² – 460P + 52900 = −42000 + 52900

(P – 230)² = 10900

Paso 4 Aplica la raíz cuadrada en ambos lados:

P – 230 = ±√10900 = ±104 (redondeado en unidades)

Paso 5 Resta (-230) de ambos lados (en otras palabras, suma 230):

P = 230 ± 104 = 126 o 334

¿Qué nos dice eso? Dice que la ganancia es CERO cuando el precio es de $ 126 o $ 334

Pero queremos saber el máximo beneficio, ¿no?

¡Está exactamente a mitad de camino! A $230

Y aquí está la gráfica:

gráfica de venta de bicicletas. Valor óptimo
Ganancia = −200P² + 92,000P − 8,400,000

El mejor precio de venta es de $ 230, y puedes esperar:

Unidades vendidas = 70,000 − 200 x 230 = 24,000
Ventas en dólares = $230 x 24,000 = $5,520,000
Costos = 700,000 + $110 x 24,000 = $3,340,000
Ganancia = $5,520,000 − $3,340,000 = $2,180,000

Una empresa muy rentable.

Ejemplo: marco de acero pequeño

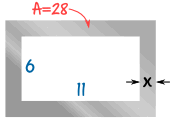
área=28

Tu empresa va a hacer marcos como parte de un nuevo producto que están lanzando.

El marco se cortará de una pieza de acero, y para mantener el peso bajo, el área final debe ser 28 cm²

El interior del marco tiene que ser de 11 cm por 6 cm

¿Cuál debería ser el ancho x del metal?

Área de acero antes del corte:

Área = (11 + 2x) × (6 + 2x) cm²

Área = 66 + 22x + 12x + 4x²

Área = 4x² + 34x + 66

Área de acero después de cortar el centro de 11 × 6:

Área = 4x² + 34x + 66 − 66

Área = 4x² + 34x

cuadrática 4x^2 + 34x

¡Vamos a resolverlo gráficamente!

Aquí está la gráfica de 4x² + 34x :

El área deseada de 28 se muestra como una línea horizontal.

El área es igual 28 cm² cuando:

x es aproximadamente −9.3 o 0.8

El valor negativo de x no tiene sentido, por lo que la respuesta es:

x = 0.8 cm (aprox.)

Ejemplo: un crucero por el río

Ejemplo: Un crucero por el río de 3 horas recorre 15 km río arriba y luego de regreso. El río tiene una corriente de 2 km por hora. ¿Cuál es la rapidez del barco y cuánto duró el viaje aguas arriba?

Bote en un río. Ida y vuelta en 3 horas

Hay dos rapideces para considerar: la rapidez que tiene el barco en el agua y la rapidez relativa a la tierra:

Sea x = la rapidez del barco en el agua (km/h)
Sea v = la rapidez relativa a la tierra (km/h)

Porque el río fluye río abajo a 2 km/h:

cuando el barco va río arriba, v = x−2 (su rapidez se reduce 2 km/h)
cuando el barco va río abajo, v = x+2 (su rapidez aumenta 2 km/h)

Podemos convertir esas rapideces en tiempos usando:

tiempo = distancia / rapidez

(moviéndose 8 km a 4 km/h toma 8/4 = 2 horas, ¿cierto?)

Y sabemos que el tiempo total es de 3 horas:

tiempo total = tiempo río arriba + tiempo río abajo = 3 horas

Pon todo eso junto:

tiempo total = 15/(x−2) + 15/(x+2) = 3 horas

Ahora usamos nuestras habilidades de álgebra para hallar "x".

Primero, deshazte de las fracciones multiplicando por (x−2)(x+2):

3(x−2)(x+2) = 15(x+2) + 15(x-2)

Desarrolla todo:

3(x²−4)= 15x+30 + 15x-30

Trae todo a la izquierda y simplifica:

3x² - 30x -12 = 0

¡Es una ecuación cuadrática! Vamos a resolverla usando la Fórmula Cuadrática:

Formula Cuadrática: x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a

Donde a, b y c son de la
Ecuación Cuadrática en "Forma Estándar": ax² + bx + c = 0

Resolver 3x² - 30x - 12 = 0

Los coeficientes son:a = 3, b = −30 y c = −12

Fórmula:x = [ −b ± √(b²−4ac) ] / 2a

Pon a, b y c:x = [ −(−30) ± √((−30)²−4×3×(−12)) ] / (2×3)

Resuelve:x = [ 30 ± √(900+144) ] / 6

x = [ 30 ± √(1044) ] / 6

x = ( 30 ± 32.31 ) / 6

x = −0.39 o 10.39

Respuesta: x = −0.39 o 10.39 (a 2 decimales)

x = −0.39 no tiene sentido para esta pregunta del mundo real, ¡pero x = 10.39 es simplemente perfecta!

Respuesta: Rapidez del bote = 10.39 km/h (a 2 decimales)

Y así, el viaje aguas arriba = 15 / (10.39−2) = 1.79 horas = 1 hora 47min
Y el viaje aguas abajo = 15 / (10.39+2) = 1.21 horas = 1 hora 13min

Ejemplo: resistencias en paralelo

Dos resistencias están en paralelo, como en este diagrama:

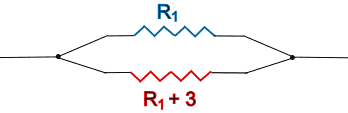
resistencias cuadráticas R1 y R1+3

La resistencia total se ha medido a 2 Ohms, y se sabe que una de las resistencias es 3 Ohms más que la otra.

¿Cuáles son los valores de las dos resistencias?

La fórmula para resolver la resistencia total "R_T" es:

1R_T = 1R₁ + 1R₂

En este caso, se tiene R_T = 2 y R₂ = R₁ + 3

1 2 = 1 R₁ + 1 R₁+3

Para deshacernos de las fracciones, podemos multiplicar todos los términos por 2R₁(R₁ + 3) y luego simplificar:

Multiplica todo por 2R₁(R₁ + 3):2R₁(R₁+3)2 = 2R₁(R₁+3)R₁ + 2R₁(R₁+3)R₁+3

Luego simplifica:R₁(R₁ + 3) = 2(R₁ + 3) + 2R₁

Desarrolla: R₁² + 3R₁ = 2R₁ + 6 + 2R₁

Pasa todo al lado izquierdo:R₁² + 3R₁ − 2R₁ − 6 − 2R₁ = 0

Simplifica:R₁² − R₁ − 6 = 0

¡Sí! ¡Una ecuación cuadrática!

Resolvámosla usando nuestro Solucionador de Ecuaciones Cuadráticas.

Pon 1, −1 y −6
Y deberías obtener las respuestas −2 y 3

R₁ no puede ser negativa, así que R₁ = 3 Ohms es la respuesta.

Las dos resistencias son de 3 ohms y 6 ohms.

Otros

Las ecuaciones cuadráticas son útiles en muchas otras áreas:

antena parabólica

Para un espejo parabólico, un telescopio reflector o una antena parabólica, la forma se define mediante una ecuación cuadrática.

Las ecuaciones cuadráticas también son necesarias cuando se estudian lentes y espejos curvos.

Y muchas preguntas que involucran tiempo, distancia y velocidad necesitan ecuaciones cuadráticas.