Graficando Ecuaciones Cuadráticas

Una Ecuación Cuadrática en Forma Estándar
(a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.)

Aquí hay un ejemplo:

Ecuación cuadrática

Graficar

Puede graficar una ecuación cuadrática usando la Graficadora de Funciones, pero para comprender realmente lo que está sucediendo, es mejor que puedas hacer la gráfica tu mismo. ¡Sigue leyendo!

La cuadrática más simple

La ecuación cuadrática más simple es:

f(x) = x²

Y su gráfica también es simple:

Square function

Ésta es la curva f(x) = x²
Es una parábola.

Ahora veamos qué sucede cuando añadimos el valor "a":

f(x) = ax²

ax^2

Los valores más grandes de a aplastan la curva hacia adentro
Los valores más pequeños de a la expanden hacia afuera
Y los valores negativos de a la voltean al revés

Juega con ella

Ahora es un buen momento para "Explorar Ecuaciones Cuadráticas"
para que puedas ver lo qué hacen diferentes valores de a, b y c.

La cuadrática "general"

Antes de graficar, reorganizamos la ecuación, a partir de esto:

f(x) = ax² + bx + c

A esto:

f(x) = a(x-h)² + k

Donde:

h = −b/2a

k = f( h )

En otras palabras, se calcula h (= −b/2a),y luego se encuentra k calculando toda la ecuación en x=h

¿Pero por qué?

vértice de una cuadrática

Lo maravilloso de esta nueva forma es que h y k nos muestran el punto más bajo (o más alto), llamado vértice:

Y también la curva es simétrica (imagen espejo) sobre el eje que pasa a través de x=h, lo que facilita la representación gráfica

Entonces...

h nos muestra qué tan a la izquierda (o derecha) se ha desplazado la curva de x=0
k nos muestra qué tan arriba (o abajo) se ha desplazado la curva de y=0

Veamos un ejemplo de cómo hacer esto:

Ejemplo: Graficar f(x) = 2x²- 12x + 16

Primero, anotemos

a = 2,
b = −12, y
c = 16

Ahora, ¿qué sabemos?

a es positivo, por lo que es una gráfica "hacia arriba" (en forma de "U")
a es 2, por lo que está un poco "aplastada" en comparación con el gráfico x²

A continuación, calculemos h:

h = −b/2a = −(−12)/(2x2) = 3

Y luego podemos calcular k (usando h=3):

k = f(3) = 2(3)² - 12·3 + 16 = 18−36+16 = −2

Así que ahora podemos trazar la gráfica (¡con comprensión real!):

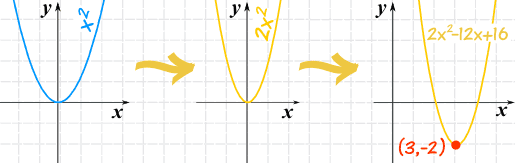
2x^2-12x+16

También sabemos: el vértice es (3,−2), y el eje es x=3

De un gráfico a la ecuación

¿Qué pasa si tenemos una gráfica y queremos encontrar una ecuación?

Ejemplo: acabas de graficar algunos datos interesantes y parece algo cuadrático:

puntos en una gráfica (0,1.5) y (1,1)

Solo conociendo esos dos puntos podemos llegar a una ecuación.

En primer lugar, sabemos h y k (en el vértice):

(h, k) = (1,1)

Así que pongamos eso en esta forma de la ecuación:

f(x) = a(x-h)² + k

f(x) = a(x−1)² + 1

Luego calculemos "a":

Tenemos el valor (0, 1.5) así que:f(0) = 1.5

Y a(x−1)² + 1 en x=0 es:f(0) = a(0−1)² + 1

Ambos son f(0) así que los igualamos: a(0−1)² + 1 = 1.5

Simplificamos:a + 1 = 1.5

a = 0.5

Y aquí está la ecuación cuadrática resultante:

f(x) = 0.5(x−1)² + 1

Nota: Puede que esta no sea la ecuación correcta para los datos, pero es un buen modelo y lo mejor que podemos encontrar.

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).