Ecuaciones Cuadráticas

Un ejemplo de una Ecuación Cuadrática:

Ecuación Cuadrática 5x^2 - 3x + 3 = 0

Las Ecuaciones Cuadráticas hacen curvas bonitas, como ésta:

Name

La palabra cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un NOTAcuadrado (en otras palabras x²).

También se les llama "Ecuaciones de Segundo NOTAGrado" (debido al "2" sobre la x).

Forma estándar

La Forma estándar de una Ecuación Cuadrática se ve parecida a esto:

ax^2 + bx + c = 0

a, b y c son valores conocidos. a no puede ser 0.

"x" es la variable o incógnita (todavía no sabemos su valor).

Aquí unos ejemplos:

2x² + 5x + 3 = 0		En ésta a=2, b=5 y c=3

x² − 3x = 0		Ésta es un poquito especial: ¿Dónde está la a? Bueno, a=1, dado que normalmente no escribimos "1x²" b = −3 ¿Y la c? Bueno, c=0, por lo que no se muestra.
5x − 3 = 0		¡Ups! Ésta no es una ecuación cuadrática: le falta x² (en otras palabras, si a=0, entonces la ecuación no es cuadrática)

¡Juega!

Juega con el "Graficador de Ecuaciones Cuadráticas" para que puedas ver:

la gráfica que se forma, y
las soluciones (llamadas "raíces").

¡Ecuaciones Cuadráticas Disfrazadas!

Como vimos antes, la Forma Estándar de una Ecuación Cuadrática es

ax² + bx + c = 0

¡Pero a veces una ecuación cuadrática se ve diferente!

Por ejemplo:

Cuadrática Disfrazada		En Forma Estándar	a, b y c
x² = 3x − 1	Mueve todos los términos a la izquierda	x² − 3x + 1 = 0	a=1, b=−3, c=1
2(w² − 2w) = 5	Desarrolla (quita los paréntesis), y mueve el 5 a la izquierda	2w² − 4w − 5 = 0	a=2, b=−4, c=−5
z(z−1) = 3	Desarrolla y mueve el 3 a la izquierda	z² − z − 3 = 0	a=1, b=−1, c=−3

¿Cómo encontramos la solución?

Las "soluciones" de una Ecuación Cuadrática son los valores donde la ecuación es igual a cero.

También se les llama "raíces", o incluso "ceros".

Gráfica Cuadrática

Normalmente hay 2 soluciones (como se muestra en la gráfica).

Y hay diferentes métodos para encontrar las soluciones:

Podemos Factorizar el Cuadrático (encontrar qué es lo que hay que multiplicar para generar la ecuación cuadrática).

O podemos Completar el Cuadrado.

O podemos usar la famosa Fórmula Cuadrática:

Fórmula: x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a

Tan solo pon los valores de a, b y c, y haz las operaciones.

Veremos este método con mayor detalle a continuación.

Acerca de la Fórmula Cuadrática

Más/Menos

Primero que nada, ¿qué es ese símbolo de más/menos que se ve así ± ?

El signo ± significa que hay DOS respuestas:

x = −b + √(b²− 4ac) 2a

x = −b − √(b²− 4ac) 2a

Aquí hay un ejemplo con dos respuestas:

Gráfica Cuadrática

¡Pero no siempre se ve así!

Imagina si la curva "solo toca" el eje-x.
¡O imagina que la curva está tan arriba que ni siquiera cruza al eje-x!

Es aquí cuando el "Discriminante" nos ayuda ...

Discriminante

¿Ves la parte donde dice b² − 4ac en la fórmula de arriba? Se llama Discriminante, porque puede "discriminar" entre los posibles tipos de respuesta:

cuando b² − 4ac es positivo, obtenemos dos soluciones reales
si es cero, sólo hay UNA solución real (en realidad las dos soluciones son la misma)
cuando es negativo, obtenemos un par de soluciones complejas

¿Soluciones complejas? Hablaremos de ellas después de que aprendamos a usar la fórmula.

El uso de la Fórmula Cuadrática

Para resolverla, solo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos.

Ejemplo: Resuelve 5x² + 6x + 1 = 0

Los coeficientes son:a = 5, b = 6, c = 1

Fórmula cuadrática:x = −b ± √(b²− 4ac) 2a

Pon los valores de a, b y c.x = −6 ± √(6²− 4×5×1) 2×5

Resuelve:x = −6 ± √(36− 20) 10

x = −6 ± √(16) 10

x = −6 ± 4 10

x = −0.2 ó −1

5x^2+6x+1

Respuesta: x = −0.2 o x = −1

Las podemos ver en esta gráfica

Comprobación -0.2:		5×(−0.2)² + 6×(−0.2) + 1 = 5×(0.04) + 6×(−0.2) + 1 = 0.2 − 1.2 + 1 = 0
Comprobación -1:		5×(−1)² + 6×(−1) + 1 = 5×(1) + 6×(−1) + 1 = 5 − 6 + 1 = 0

¿Soluciones Complejas?

Cuando el discriminante (el valor de b² − 4ac) es negativo obtenemos un par de respuestas Complejas ... ¿Qué significa eso?

Significa que nuestra respuesta incluye Números Imaginarios. ¡Wow!

Ejemplo: Resuelve 5x² + 2x + 1 = 0

Los coeficientes son:a=5, b=2, c=1

Observa que el discriminante es negativo:b² − 4ac = 2² − 4×5×1
= −16

Usa la fórmula cuadrática:x = −2 ± √(−16) 10

√(−16) = 4i
(donde i es el número imaginario √−1)

Por lo tanto:x = −2 ± 4i 10

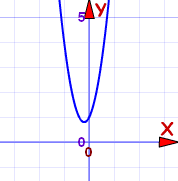
5x^2+2x+1

Respuesta: x = −0.2 ± 0.4i

La curva no cruza al eje-x. Ésa es la razón por la que vemos números complejos en la respuesta.

De cierta forma es un poco más fácil: ya no necesitamos hacer más operaciones, solo dejamos la respuesta como −0.2 ± 0.4i.

Ejemplo: Resuelve x² − 4x + 6.25 = 0

Los coeficientes son:a=1, b=−4, c=6.25

Observa que el discriminante es negativo:b² − 4ac = (−4)² − 4×1×6.25
= −9

Usa la fórmula cuadrática:x = −(−4) ± √(−9) 2

√(−9) = 3i
(donde i es el número imaginario √−1)

Nos queda:x = 4 ± 3i 2

Gráfica de una Ecuación Cuadrática con Raíces Complejas

Respuesta: x = 2 ± 1.5i

La curva no cruza al eje-x. Ésa es la razón por la que vemos números complejos en la respuesta.

Gráfica de una Ecuación Cuadrática con Raíces Complejas-2

PERO una imagen espejo arriba/abajo de nuestra ecuación sí que cruza el eje-x en 2 ± 1.5 (nota: no hay i).

¡Un dato interesante para ti!

Resumen

Ecuación Cuadrática en Forma Estándar: ax² + bx + c = 0
Las ecuaciones cuadráticas pueden ser factorizadas
Fórmula Cuadrática: x = −b ± √(b²− 4ac) 2a
Cuando el Discriminante (b²−4ac) es:
- positivo, hay 2 soluciones reales
- cero, hay 1 solución real
- negativo, hay 2 soluciones complejas

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

(Hard Questions: 1 2 3 4 5 6 7 8 )