Transformaciones y Matrices
¡Una matriz puede hacer transformaciones geométricas!
Juega con esta aplicación de transformación 2D:
Las matrices también pueden transformar de 3D a 2D (muy útil para gráficos por computadora), hacer transformaciones en 3D y mucho más.
Las matemáticas
Para cada punto [x, y] que conforma la figura, hacemos esta multiplicación de matrices:
Cuando la matriz de transformación [a, b, c, d] es la matriz identidad (el equivalente matricial del número "1") los valores [x, y] no cambian:
Cambiar el valor "b" conduce a una transformación "inclinada" (pruébalo arriba):
Y ésta hará un "giro" diagonal sobre la línea x = y (pruébalo también):
¿Qué más puedes descubrir?
Muchas transformaciones a la vez
Podemos "encadenar" transformaciones mediante multiplicación de matrices.
Ejemplo: un giro diagonal seguido de una inclinación horizontal:
¡Ten cuidado! Las transformaciones van de derecha a izquierda, por lo que es inclinación × giro = "girar luego inclinar"
Y luego podemos usar ese resultado en una transformación:
Hace estas dos transformaciones a la vez:
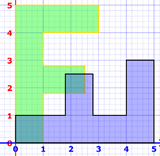 luego
luego 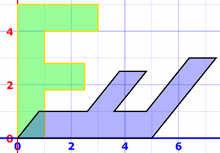
Ejemplo: una inclinación horizontal seguida de un giro diagonal:
Recuerda que el orden es giro × inclinación = "inclinar luego girar"
¡Es un resultado diferente!
Hace estas dos transformaciones a la vez:
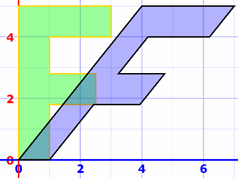 luego
luego 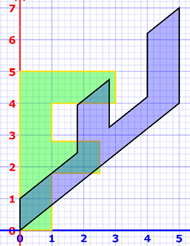
¡Pero tenemos que tener cuidado en qué orden hacemos las transformaciones!
También nos muestra por qué es importante el orden de multiplicar las matrices (a diferencia de los números ordinarios que pueden multiplicarse en cualquier orden, por ejemplo 2×3 = 3×2).
Transforma en código
¿Necesitas escribir el código? Aquí te digo cómo.La letra F es solo una lista de coordenadas:
[3, 4], [3, 5], [0, 5], [0, 0], [1, 0], [1, 1.8], [2.5, 1.8], [2.5, 2.8], [1, 2.8], [1, 4]
Y recorremos esos puntos, creando nuevos puntos usando la matriz 2×2 "a, b, c, d":
for (var i = 0; i < shape.pts.length; i++) {
var pt = shape.pts[i]
var x = a * pt[0] + b * pt[1]
var y = c * pt[0] + d * pt[1]
newPts.push({ x: x, y: y })
}
¡Luego graficamos los puntos originales y los puntos transformados para que podamos ver ambos!
Rotación
Para rotar simplemente usa esta matriz:
Ejemplo: Rota por 30°
Cálculo a 4 decimales:
¡Pruébalo en la aplicación en la parte superior!
Y probémoslo en un punto aquí:
Y obtenemos esto:
Nota al pie: intercambio de filas y columnas
¡Las matrices son flexibles!Esta transformación inclinada:
Se puede hacer así:
Las filas y columnas se intercambian todas (transpuesta),y el orden de multiplicación se invierte, pero aún funciona. Solo para que lo sepas.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
