Resolver Triángulos AAL
"AAL" significa "Ángulo, Ángulo, Lado"
|
"AAL" es cuando conocemos dos ángulos y un lado (que no está entre los ángulos). |
|
Para resolver un triángulo AAL
|
Ejemplo 1
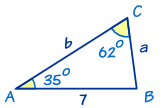
En este triángulo conocemos:
- ángulo A = 35°
- ángulo C = 62°
- y lado c = 7
Es fácil encontrar el ángulo B usando que 'los ángulos de un triángulo suman 180°':
B = 180° − 35° − 62° = 83°
También podemos encontrar el lado a usando La Ley de los Senos:
a/sin A = c/sin C
a/sin(35°) = 7/sin(62°)
a = (7 × sin(35°))/sin(62°)
a = 4.55 a 2 decimales
También podemos encontrar b usando La Ley de los Senos:
b/sin B = c/sin C
b/sin(83°) = 7/sin(62°)
b = (7 × sin(83°))/sin(62°)
b = 7.87 a 2 decimales
¡Ahora hemos resuelto completamente el triángulo!
¿Te diste cuenta que usamos b/sin B = c/sin C en lugar de b/sin B = a/sin A para las últimas operaciones?
Hay una buena razón para eso. ¿Qué pasa si cometemos un error al encontrar a? ¡Entonces nuestra respuesta para b también estaría mal!Como regla general, siempre es mejor usar los lados y ángulos que se dan en lugar de los que acabamos de resolver.
Ejemplo 2
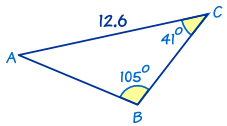
Este también es un triángulo AAL.
Primero, hallamos el ángulo A usando que 'los ángulos de un triángulo suman 180°':
Ahora encuentra el lado c usando La ley de los senos:
De manera similar, podemos encontrar el lado a usando La ley de los senos y usando el lado dado b = 12.6 en lugar de c que acabamos de resolver:
¡Listo!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
