La Ley de Senos
La Ley de Senos (o Regla de Senos) es muy útil para resolver triángulos:
a sin A = b sin B = c sin C
Funciona para cualquier triángulo:
|
a, b y c son lados. A, B y C son ángulos. (El lado a está frente al ángulo A, |
Y dice que:
Cuando dividimos el lado a por el seno del ángulo A
es igual al lado b dividido por el seno del ángulo B,
y también igual al lado c dividido por el seno del ángulo C
¿Será cierto todo eso?
Bueno, hagamos los cálculos para un triángulo que diseñé anteriormente:
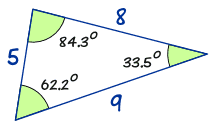 |
a sin A = 8 sin(62.2°) = 8 0.885... = 9.04... b sin B = 5 sin(33.5°) = 5 0.552... = 9.06... c sin C = 9 sin(84.3°) = 9 0.995... = 9.04... |
¡Las respuestas son casi las mismas!
(Serían exactamente iguales si utilizáramos precisión
perfecta).
Así que:
a sin A = b sin B = c sin C
¿Esto es magia?
En realidad no, mira este triángulo general e imagina que son dos triángulos en ángulo recto que comparten el lado h:
El seno de un ángulo es el opuesto dividido por la hipotenusa, entonces:
| sin(A) = h/b |  |
b sin(A) = h | |
| sin(B) = h/a |  |
a sin(B) = h |
a sin(B) y b sin(A) ambos son iguales a h, por lo que tenemos:
a sin(B) = b sin(A)
Que se puede reorganizar así:
a sin A = b sin B
Podemos seguir pasos similares para incluir c/sin (C)
¿Cómo se usa?
Veamos con un ejemplo.
Ejemplo: Hallar el lado "c"
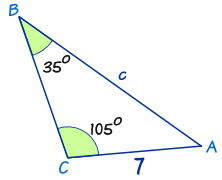
Ahora usa tus habilidades de álgebra para reorganizar y resolver:
Encontrar un ángulo desconocido
En el ejemplo anterior encontramos un lado desconocido ...
... pero también podemos usar la Ley de Senos para encontrar un ángulo desconocido.
En este caso, es mejor invertir las fracciones (sin A/a en lugar de a/sin A, etc):
sin A a = sin B b = sin C c
Ejemplo: Hallar el ángulo B
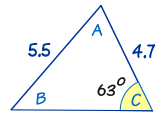
¡A veces hay dos respuestas!
Hay un detalle engañoso que debemos tener en cuenta:
Dos posibles respuestas.
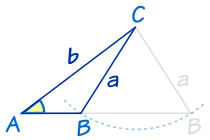 |
Imagina que conocemos el ángulo A, y los lados a y b. Podemos girar el lado a hacia la izquierda o la derecha y obtener dos resultados posibles (un triángulo pequeño y un triángulo mucho más ancho)¡Ambas respuestas son correctas!
|
Esto solo ocurre en el caso "Dos
Lados Y Un Ángulo Que No Está Entre Ellos", e incluso en
ese caso no siempre ocurre, pero tenemos que estar atentos.
Solo piensa "¿podría mover ese lado hacia otra parte y también tener una
respuesta correcta?"
Ejemplo: Hallar el ángulo R
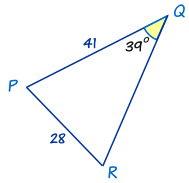
Lo primero que debe notar es que este triángulo tiene diferentes etiquetas: PQR en lugar de ABC. Pero eso esta bien. Solo usamos P, Q y R en lugar de A, B y C en La Ley de Senos.
La calculadora no te dirá esto, pero sin (112.9°) también es igual a 0.9215 ...
Entonces, ¿cómo descubrimos el valor 112.9°?
Fácil ... mueve 67.1° de 180°, así:
180° − 67.1° = 112.9°
Entonces hay dos respuestas posibles para R: 67.1° y 112.9°:
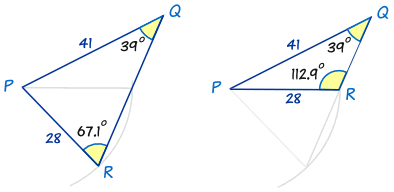
¡Ambos son posibles! Cada uno tiene el ángulo de 39° y lados de 41 y 28.
Por lo tanto, siempre verifica si la respuesta alternativa tiene sentido.
- ... a veces tendrá sentido (como en el caso de arriba) y habrá dos soluciones
- ... a veces no tendrá sentido (mira abajo) y habrá solo una solución
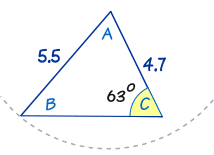 |
Ya vimos este triángulo antes. Como puedes ver, puedes intentar "columpiar" el lado "5.5", pero ninguna otra solución tiene sentido. Entonces este solo tiene una solución. |
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
