Ley de Cosenos

Para cualquier triángulo:

a, b y c son los lados.

C es el ángulo opuesto al lado c

La Ley de los Cosenos (también llamada la Regla de los Cosenos) dice:

c² = a² + b² − 2ab cos(C)

Nos ayuda a resolver algunos triángulos. Veamos cómo usarla.

Ejemplo: ¿Cuánto mide el lado "c" ...?

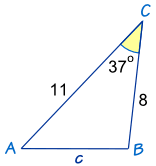
ejemplo de ley de cosenos

Conocemos el ángulo C = 37º y los lados a = 8 y b = 11

La ley de los cosenos dice:c² = a² + b² − 2ab cos(C)

Pon los valores que conocemos:c² = 8² + 11² − 2 × 8 × 11 × cos(37º)

Haz unas operaciones:c² = 64 + 121 − 176 × 0.798…

Más operaciones:c² = 44.44...

Toma la raíz cuadrada:c = √44.44 = 6.67 a 2 decimales

Respuesta: c = 6.67

Cómo recordar

¿Cómo puedes recordar la fórmula?

Bueno, ayuda saber que es el Teorema de Pitágoras con algo extra para que funcione para todos los triángulos:

Teorema de Pitágoras:
(solo para triángulos rectángulos)a² + b² = c²

Ley de Cosenos:
(para todos los triángulos)a² + b² − 2ab cos(C) = c²

Entonces, para recordarla:

piensa "abc": a² + b² = c²,
luego un 2do "abc": 2ab cos(C),
y pon todo junto: a² + b² − 2ab cos(C) = c²

Cuando usarla

La Ley de cosenos es útil para encontrar:

el tercer lado de un triángulo cuando conocemos dos lados y el ángulo entre ellos (como en el ejemplo anterior)
los ángulos de un triángulo cuando conocemos los tres lados (como en el siguiente ejemplo)

Ejemplo: ¿Cuánto mide el ángulo "C" ...?

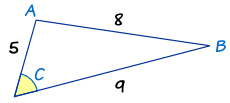
ley de cosenos ejemplo

El lado de longitud "8" es el ángulo opuesto C, por lo que es el lado c. Los otros dos lados son a y b.

Ahora pongamos lo que sabemos en La Ley de Cosenos:

Empieza por:c² = a² + b² − 2ab cos(C)

Pon a, b y c:8² = 9² + 5²− 2 × 9 × 5 × cos(C)

Calcula:64 = 81 + 25− 90 × cos(C)

Ahora usamos nuestras habilidades de álgebra para reorganizar y resolver:

Resta 25 de ambos lados:39 = 81− 90 × cos(C)

Resta 81 de ambos lados:−42 = −90 × cos(C)

Voltea:−90 × cos(C) = −42

Divide ambos lados entre −90:cos(C) = 42/90

Arco-coseno:C = cos⁻¹(42/90)

Calculadora:C = 62.2° (a 1 decimal)

En otras formas

Versión más fácil para ángulos

Acabamos de ver cómo encontrar un ángulo cuando conocemos tres lados. Tomó bastantes pasos, por lo que es más fácil usar la fórmula "directa" (que es solo una reorganización de la fórmula c² = a² + b² − 2ab cos(C)). Puede estar en cualquiera de estas formas:

cos(C) = a² + b² − c² 2ab

cos(A) = b² + c² − a² 2bc

cos(B) = c² + a² − b² 2ca

Ejemplo: encontrar el ángulo "C" usando la ley de los cosenos (versión para ángulos)

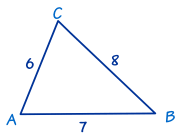
triángulo LLL

En este triángulo conocemos los tres lados:

a = 8,
b = 6 y
c = 7.

Usa la Ley de Cosenos (versión para ángulos) para encontrar el ángulo C :

cos C= (a² + b² − c²)/2ab

= (8² + 6² − 7²)/2×8×6

= (64 + 36 − 49)/96

= 51/96

= 0.53125

C= cos⁻¹(0.53125)

= 57.9° a 1 decimal

Versiones para a, b y c

Además, podemos reescribir la fórmula c² = a² + b² − 2ab cos(C) para tener a²= y b²=.

Aquí están las tres:

a² = b² + c² − 2bc cos(A)

b² = a² + c² − 2ac cos(B)

c² = a² + b² − 2ab cos(C)

¡Pero es más fácil recordar la forma "c² =" y cambiar las letras según sea necesario!

Como en este ejemplo:

Ejemplo: Encuentra la distancia "z"

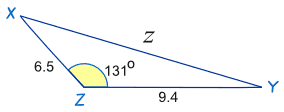
ley de cosenos ejemplo

¡Las letras son diferentes! Pero eso no importa. Podemos sustituir fácilmente x por a, y por b y z por c

Empieza con:c² = a² + b² − 2ab cos(C)

x por a, y por b y z por c:z² = x² + y² − 2xy cos(Z)

Pon los valores que conocemos:z² = 9.4² + 6.5² − 2×9.4×6.5×cos(131º)

Calcula:z² = 88.36 + 42.25 − 122.2 × (−0.656...)

z² = 130.61 + 80.17...

z² = 210.78...

z = √210.78... = 14.5 a 1 decimal.

Respuesta: z = 14.5

¿Notaste que cos(131º) es negativo y esto cambia el último signo del cálculo a + (positivo)? El coseno de un ángulo obtuso siempre es negativo (ver Círculo Unitario).

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).