Resolver Triángulos ALA

Ejemplo 1

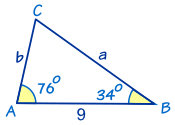
En este triángulo conocemos:

• ángulo A = 76°
• ángulo B = 34°
• y c = 9

 

Es fácil encontrar el ángulo C usando que 'los ángulos de un triángulo suman 180°':

So C = 180° − 76° − 34° = 70°

 

También podemos encontrar el lado a usando La Ley de los Senos:

a/sinA = c/sin C

a/sin76° = 9/sin70°

a = (9/sin70°) × sin76°
a = 9.29 a 2 decimales

 

Análogamente, podemos encontrar el lado b usando La Ley de los Senos

b/sinB = c/sin C

b/sin34° = 9/sin70°

b = (9/sin70°) × sin34°
b = 5.36 a 2 decimales

 

Ahora hemos resuelto completamente el triángulo, es decir, hemos encontrado todos sus ángulos y lados.

Ejemplo 2

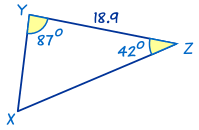
Este también es un triángulo ALA.

Primero hay que encontrar el ángulo X usando que 'los ángulos de un triángulo suman 180°':

X = 180° − 87° − 42° = 51°

Ahora podemos encontrar el lado y usando La Ley de los Senos:

y/sinY = x/sin X

y/sin(87°) = 18.9/sin(51°)

y = (18.9/sin(51°)) × sin(87°)
y = 24.29 a 2 decimales.

Análogamente encontramos el lado z usando La Ley de los Senos

z/sinZ = x/sin X

z/sin(42°) = 18.9/sin(51°)

z = (18.9/sin(51°)) × sin(42°)
z = 16.27 a 2 decimales.