Resolver Triángulos LLL

"LLL" significa "Lado, Lado, Lado"

triángulo LLL

"LLL" es cuando conocemos tres lados del triángulo y queremos encontrar los ángulos faltantes.

Para resolver un triángulo LLL:

Usamos la versión "angular" de la Ley de Cosenos:

cos(C) = a2 + b2 − c22ab

cos(A) = b2 + c2 − a22bc

cos(B) = c2 + a2 − b22ca

(todas son la misma fórmula, solo letras diferentes)

Primero, comprueba que los tres lados formen un triángulo. Los dos lados más cortos juntos deben ser más largos que el lado más largo.

Ejemplo 1

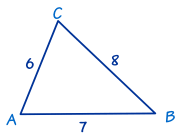
ejemplo triángulo LLL 6,7,8

En este triángulo conocemos los tres lados:

  • a = 8,
  • b = 6 y
  • c = 7.

Usa primeramente la Ley de Cosenos para encontrar uno de los ángulos. No importa cuál. Primero encontremos el ángulo A:

cos A = (b2 + c2 − a2) / 2bc
cos A = (62 + 72 − 82) / (2×6×7)
cos A = (36 + 49 − 64) / 84
cos A = 0.25
A = cos−1(0.25)
A = 75.5224...°
A = 75.5° a 1 decimal.

A continuación encontraremos otro lado. Usamos la Ley de Cosenos nuevamente, esta vez para el ángulo B:

cos B = (c2 + a2 − b2)/2ca
cos B = (72 + 82 − 62)/(2×7×8)
cos B = (49 + 64 − 36) / 112
cos B = 0.6875
B = cos−1(0.6875)
B = 46.5674...°
B = 46.6° a 1 decimal

Ahora usaremos que "los tres ángulos suman 180°" para encontrar el ángulo C:

C = 180° − 75.5224...° − 46.5674...°
C = 57.9° a 1 decimal

Ahora hemos resuelto completamente el triángulo, es decir, hemos encontrado todos sus ángulos.

El triángulo puede tener letras que no sean ABC:

Ejemplo 2

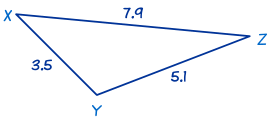
triángulo LLL 3.5, 5.1, 7.9

Este también es un triángulo LLL.

En este triángulo conocemos los tres lados x = 5.1, y = 7.9 y z = 3.5. Usa la Ley de Cosenos para encontrar primeramente el ángulo X:

cos X = (y2 + z2 − x2)/2yz
cos X = ((7.9)2 + (3.5)2 − (5.1)2)/(2×7.9×3.5)
cos X = (62.41 + 12.25 − 26.01)/55.3
cos X = 48.65/55.3 = 0.8797...
X = cos−1(0.8797...)
X = 28.3881...°
X = 28.4° a 1 decimal

Luego usaremos la Ley de Cosenos nuevamente para encontrar el ángulo Y:

cos Y = (z2 + x2 − y2)/2zx
cos Y = −24.15/35.7 = −0.6764...
cos Y = (12.25 + 26.01 − 62.41)/35.7
cos Y = −24.15/35.7 = −0.6764...
Y = cos−1(−0.6764...)
Y = 132.5684...°
Y = 132.6° a 1 decimal.

Finalmente usaremos que "los tres ángulos suman 180°" para encontrar el ángulo Z:

Z = 180° − 28.3881...° − 132.5684...°
Z = 19.0° a 1 decimal

Otro método

Aquí hay otra forma (un poco más rápida) de resolver un triángulo LLL:

¿El ángulo más grande?

¿Por qué tratamos de encontrar el ángulo más grande primero? De esa manera, los otros dos ángulos deben ser agudos (menos de 90°) y la Ley de Senos dará respuestas correctas.

La Ley de Senos es difícil de usar con ángulos mayores de 90°. Puede haber dos respuestas a cada lado de 90° (ejemplo: 95° y 85°), pero una calculadora solo dará la respuesta más pequeña.

Entonces, al calcular el ángulo más grande primero usando la Ley de Cosenos, los otros ángulos son menores de 90° y la Ley de Senos se puede usar en cualquiera de ellos sin dificultad.

Ejemplo 3

triángulo LLL 7.4, 11.6, 15.2

B es el ángulo más grande, así que primero encontraremos B usando la Ley de Cosenos:

cos B = (a2 + c2 − b2) / 2ac
cos B = (11.62 + 7.42 − 15.22) / (2×11.6×7.4)
cos B = (134.56 + 54.76 − 231.04) / 171.68
cos B = −41.72 / 171.68
cos B = −0.2430...
B = 104.1° a 1 decimal

Usa la Ley de los Senos, sinC / c = sinB / b, para encontrar el ángulo A:

sin C / 7.4 = sin 104.1° / 15.2
sin C = 7.4 × sin 104.1° / 15.2
sin C = 0.4722...
C = 28.2° a 1 decimal

Usa que "los tres ángulos suman 180°" para encontrar el ángulo A:

A = 180° − (104.1° + 28.2°)
A = 180° − 132.3°
A = 47.7° a 1 decimal

Así que A = 47.7°, B = 104.1°, y C = 28.2°

Listo, y fue más fácil.


¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

 
Practica Resolver Triángulos Resolver Triángulos Índice de Trigonometría La Ley de Senos La Ley de Cosenos Índice de Álgebra