Funciones logarítmicas
Esta es la función logarítmica:
f(x) = loga(x)
a es cualquier valor mayor que 0, excepto 1
Las propiedades dependen del valor de "a"
- Cuando a=1, la gráfica no está definida
- Aparte de eso, hay dos casos a considerar:
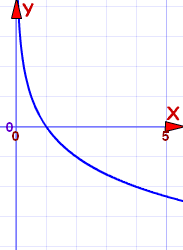
a entre 0 y 1 |
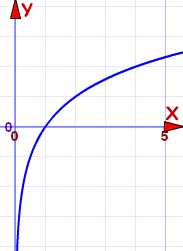
a mayor a 1 |
|
 |
 |
|
|
Ejemplo: f(x) = log½(x)
|
Ejemplo: f(x) = log2(x)
|
|
Para a entre 0 y 1
|
Para a mayor a 1:
|
Traza su gráfica aquí (modifica el valor de "a" deslizándolo)
En general, la función logarítmica:
- siempre está en el lado positivo de (y nunca cruza) el eje y
- siempre se cruza con el eje x en x=1 ... en otras palabras, pasa por (1,0)
- es igual a 1 cuando x=a, en otras palabras, pasa por (a,1)
- es una función inyectiva (uno a uno)
Su dominio son los Números Reales positivos: (0, +∞)
Su rango son los Números
Reales:
Inversa
loga(x) es la función inversa de ax (la función exponencial)
Entonces, la función logarítmica puede ser "revertida" por la función exponencial.
La función logaritmo natural
Esta es la función logaritmo "natural":
f(x) = loge(x)
Donde e es el "Número de Euler" = 2.718281828459... etc.
Pero es más común escribirla de esta manera:
f(x) = ln(x)
"ln" significa "log natural"
Así que cuando veas ln(x), solo recuerda que es la función logarítmica con base e: loge(x).
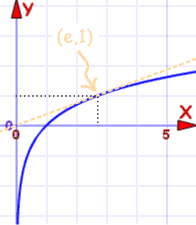
Gráfica de f(x) =
ln(x)
En el punto (e,1) la pendiente de la línea es 1/e y la recta es tangente a la curva.

