Coordenadas polares y cartesianas
... y cómo convertir de una a otra.
¿Tienes prisa? Lee el resumen. Pero te recomiendo leer toda la explicación completa:
Para indicar dónde estás en un mapa o gráfico hay dos sistemas:
Coordenadas cartesianas
Con coordenadas cartesianas señalas un punto diciendo la distancia de lado y la distancia vertical:
Coordenadas polares
Con coordenadas polares señalas un punto diciendo la distancia y el ángulo que se forma:
Convertir
Para convertir de un sistema a otro usaremos el siguiente triángulo:
De cartesianas a polares
Si tienes un punto en coordenadas cartesianas (x,y) y lo quieres en coordenadas polares (r,θ), necesitas resolver un triángulo del que conoces dos lados.
Ejemplo: ¿Cuál es el punto (12,5) en coordenadas polares?
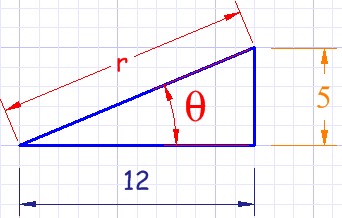
Usamos el teorema de Pitágoras para calcular el lado largo (la hipotenusa):
Usa la función tangente para calcular el ángulo:
Respuesta: el punto (12,5) es (13, 22.6°) en coordenadas polares.

¿Qué es tan-1 ?
Es la función arcotangente (a veces llamada tangente inversa):
- La tangente toma un ángulo y arroja una razón
- La arcotangente toma una razón (como "5/12") y arroja un ángulo.
Resumen: convertir de coordenadas cartesianas (x, y) a coordenadas polares (r,θ):
- r = √ ( x2 + y2 )
- θ = tan-1 ( y / x )
Nota: Las calculadoras pueden dar un valor incorrecto de tan-1 () cuando x o y son negativos ... consulta más abajo para más detalles sobre esto.
De polares a cartesianas
Si tienes un punto en coordenadas polares (r, θ) y lo quieres en coordenadas cartesianas (x,y) necesitas resolver un triángulo del que conoces el lado largo y un ángulo:Ejemplo: ¿Cuál es el punto (13, 22.6°) en coordenadas cartesianas?
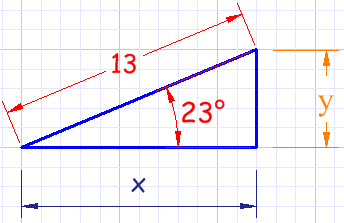
| Usamos la función coseno para x: | cos( 22.6° ) = x / 13 | |
| Cambiamos de orden y resolvemos: | x = 13 × cos( 22.6° ) | |
| x = 13 × 0.923 | ||
| x = 12.002... | ||
| Usa la función seno para y: | sin( 22.6° ) = y / 13 | |
| Cambiamos de orden y resolvemos: | y = 13 × sin( 22.6° ) | |
| y = 13 × 0.391 | ||
| y = 4.996... |
Respuesta: el punto (13, 22.6°) es casi exactamente (12, 5) en coordenadas cartesianas.
Resumen: convertir de coordenadas polares (r, θ) a coordenadas cartesianas (x,y) :
- x = r × cos( θ )
- y = r × sin( θ )
¿Cómo puedes recordarlo?
(x,y) tiene orden alfabético,
(cos, sin) también es alfabético
Pero, ¿qué pasa con los valores negativos de x y y?
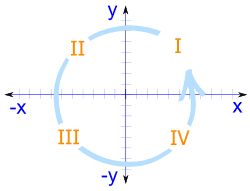
Cuatro cuadrantes
Cuando incluimos valores negativos, los ejes x y y dividen el espacio en 4 partes:
Los cuadrantes I, II, III y IV
(Están numerados en sentido antihorario)
Al convertir de coordenadas polares a cartesianas
todo funciona sin problemas:
Ejemplo: ¿Cuál es el punto (12, 195°) en coordenadas cartesianas?
r = 12 y θ = 195°
- x = 12 × cos(195°)
x = 12 × −0.9659...
x = −11.59 a 2 decimales - y = 12 × sin(195°)
y = 12 × −0.2588...
y = −3.11 a 2 decimales
Por lo que el punto está en (−11.59, −3.11), el cual queda en el Cuadrante III
Pero al convertir de coordenadas cartesianas a polares ...
... la calculadora puede dar un valor incorrecto de tan-1
¡Todo depende de en cuál Cuadrante esté el punto! Usa esto para
arreglar cosas:
| Cuadrante | Valor de tan-1 |
| I | Usa el valor de la calculadora |
| II | Suma 180° al valor de la calculadora |
| III | Suma 180° al valor de la calculadora |
| IV | Suma 360° al valor de la calculadora |
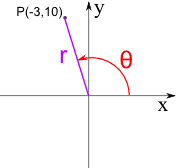
Ejemplo: P = (−3, 10)
P está en el Cuadrante II
- r = √((−3)2 + 102)
r = √109 = 10.4 a 1 decimal - θ = tan-1(10/−3)
θ = tan-1(−3.33...)
El valor de la calculadora para tan-1(−3.33...) es −73.3°
Entonces las coordenadas polares para el punto (−3, 10) son (10.4, 106.7°)
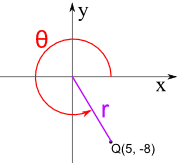
Ejemplo: Q = (5, −8)
Q está en el Cuadrante IV
- r = √(52 + (−8)2)
r = √89 = 9.4 a 1 decimal - θ = tan-1(−8/5)
θ = tan-1(−1.6)
El valor de la calculadora para tan-1(−1.6) es −58.0°
Entonces las coordenadas polares para el punto (5, −8) son (9.4, 302.0°)
Resumen
Para convertir de coordenadas polares (r, θ) a coordenadas cartesianas (x, y):
- x = r × cos( θ )
- y = r × sin( θ )
Para convertir de coordenadas cartesianas (x, y) a coordenadas polares (r, θ):
- r = √ ( x2 + y2 )
- θ = tan-1 ( y / x )
El valor de tan-1( y/x ) puede que requiera ser ajustado:
- Cuadrante I: Usa el valor de la calculadora
- Cuadrante II: Suma 180°
- Cuadrante III: Suma 180°
- Cuadrante IV: Suma 360°
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).


