Funciones Trigonométricas Inversas
En breve:
Para un triángulo rectángulo:
La función seno sin toma el ángulo θ y da la razón opuesto hipotenusa
La función inversa de seno sin-1 toma la razón opuestohipotenusa y da un ángulo θ
Y el coseno y la tangente siguen una idea similar.
Ejemplo (las longitudes están redondeadas a un decimal):
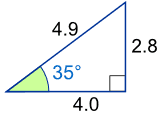
Y ahora los detalles:
Las funciones Seno, Coseno y
Tangente están basadas en un triángulo rectángulo
Son funciones muy similares ... así que veremos la función seno y
luego el seno inverso para aprender de qué se trata.
Función Seno
El Seno de un ángulo θ es:
- la longitud del lado opuesto al ángulo θ
- dividido por la longitud de la Hipotenusa
O de forma más simple:
sin(θ) = Opuesto / Hipotenusa
Ejemplo: ¿Cuál es el seno de 35°?
 |
Usando este triángulo (las longitudes están redondeadas a un decimal): sin(35°) = Opuesto / Hipotenusa |
La Función Seno puede ayudarnos a resolver cosas como esta:
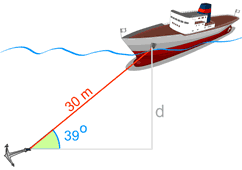
Ejemplo: Usar la función seno para encontrar "d"
Conocemos:- El ángulo que forma el cable con el fondo marino es de 39°
- La longitud del cable es de 30 m.
La profundidad "d" es 18.88 m
Función Inversa de Seno
Pero a veces es el ángulo lo que necesitamos encontrar.Aquí es donde entra el "seno inverso".
Responde a la pregunta "¿qué ángulo tiene el seno igual a opuesto/hipotenusa?"
El símbolo para la función inversa de seno es sin-1 (o sen-1), o también arcsin (o arcsen).
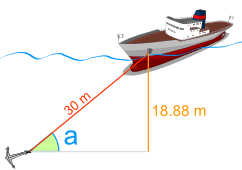
Ejemplo: Encontrar el ángulo "a"
Conocemos:
- La profundidad es 18.88 m.
- La longitud del cable es 30 m.
Y queremos hallar el ángulo "a"
¿Qué ángulo tiene un seno igual a 0.6293 ...?
El seno inverso nos lo dirá.
El ángulo "a" es 39.0°
Hacia Adelante y Hacia Atrás
- sin toma el ángulo θ y da la razón "opuesto/hipotenusa"
- sin-1 toma la razón "opuesto/hipotenusa" y nos da un ángulo.
Ejemplo:
Calculadora
 |
En la calculadora, presiona una de las siguientes opciones (según tu marca de calculadora): '2ndF sin' o 'shift sin'. |
En tu calculadora prueba a usar sin y luego sin-1 para ver qué ocurre.
¡Más de un Ángulo!
El seno inverso solo muestra un ángulo ... pero hay más ángulos que podrían funcionar.
Ejemplo: Aquí se muestran 2 ángulos tales que opuesto/hipotenusa = 0.5
De hecho, hay infinitos ángulos, porque puedes seguir sumando (o restando) 360°:
¡Recuerda esto, porque hay momentos en los que realmente necesitas uno de los otros ángulos!
Resumen
El seno de un ángulo θ es:
sin(θ) = Opuesto / Hipotenusa
Y el seno inverso es:
sin-1 (Opuesto / Hipotenusa) = θ
¿Qué pasa con "cos" y "tan" ...?
Exactamente la misma idea, pero diferentes proporciones laterales.
Coseno
El coseno de un ángulo θ es:
cos(θ) = Adyacente / Hipotenusa
Y el coseno inverso es:
cos-1 (Adyacente / Hipotenusa) = θ
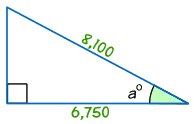
Ejemplo: Encuentra la medida del ángulo a°
cos a° = Adyacente / Hipotenusa
cos a° = 6,750/8,100 = 0.8333...
a° = cos-1 (0.8333...) = 33.6° (a 1 decimal)
Tangente
La tangente de un ángulo θ es:
tan(θ) = Opuesto / Adyacente
Así que la tangente inversa es:
tan-1 (Opuesto / Adyacente) = θ
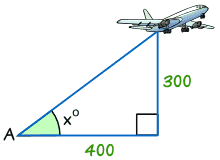
Ejemplo: Encuentra la medida del ángulo x°
tan x° = Opuesto / Adyacente
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.9° (a 1 decimal)
Otros Nombres
A veces sin-1 se conoce como sen-1,
asin/asen o arcsin/arcsen
Igualmente, cos-1 se conoce como acos o arccos
Y tan-1 se conoce como atan o arctan
Ejemplos:
- arcsen(y) es lo mismo que sen-1(y)
- atan(θ) es lo mismo que tan-1(θ)
- etc.
Las Gráficas
Y por último, aquí están las gráficas de seno, seno inverso, coseno y coseno inverso:
Seno
Seno Inverso
Coseno
Coseno Inverso
¿Notaste algo sobre las gráficas?
- Se ven similares de alguna manera, ¿verdad?
- Pero el seno inverso y el coseno inverso no "continúan para siempre" como lo hacen Seno y Coseno ...
Aquí está el coseno y el coseno inverso trazados en la misma gráfica:
Coseno y Coseno Inverso
Pero, ¿por qué el coseno inverso se corta en la parte superior e inferior (las líneas punteadas no son realmente parte de la función) ...?
Porque para
ser una función solo puede dar una respuesta
a la pregunta "¿Cuánto es cos-1(x)?"
Una respuesta o infinitas respuestas
Pero vimos anteriormente que hay infinitas respuestas, y la línea punteada en el gráfico lo muestra.Entonces sí, hay infinitas respuestas ...
... pero imagina que escribes 0.5 en tu calculadora y presionas cos-1 y te da una lista infinita de posibles resultados ...
Entonces usamos la regla de que una función solo puede dar una respuesta.
Entonces, al delimitarlo así obtenemos solo una respuesta, pero debemos recordar que podría haber otras respuestas.
Tangente y Tangente Inversa
Y aquí está la función tangente y la tangente inversa. ¿Puedes ver cómo tienen simetría (respecto a la diagonal) ...?
Tangente
Tangente Inversa
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
