Perímetro de la Elipse

En la página sobre la Elipse vimos la definición y algunas de las propiedades simples de la elipse, y aquí veremos cómo calcular con mayor precisión su perímetro.

Curiosamente, ¡el perímetro de una elipse es muy difícil de calcular!

Hay muchas fórmulas, aquí hay algunas interesantes. (Mira también la calculadora más abajo).

¡Primero mide tu elipse!

elipse ejes mayor y menor

a y b se miden desde el centro, por lo que son como medidas parecidas a un "radio".

Aproximación 1

Esta aproximación está dentro de aproximadamente el 5% del valor real, siempre que a no sea más de 3 veces más grande que b (en otras palabras, que la elipse no esté demasiado "aplastada"):

p ≈ 2π √a²+b²2

Aproximación 2

Al famoso matemático indio Ramanujan se le ocurrió esta mejor aproximación:

p ≈ π ( 3(a+b) − √(3a+b)(a+3b) )

Aproximación 3

Ramanujan también se le ocurrió esta. Primero calculamos "h":

h = (a − b)²(a + b)²

Y luego la usamos aquí:

p ≈ π(a+b) ( 1 + 3h10 + √(4−3h) )

Serie infinita 1

Esta es una fórmula exacta, pero necesita una "serie infinita" de cálculos para ser exactos, por lo que en la práctica solo obtenemos una aproximación.

Primero calculamos e (la "excentricidad", no el Número de Euler "e"):

e = √a² − b²a

Luego se usa esta fórmula de "suma infinita":

elipse perímetro aproximadamente 2a pi [1 - sigma i = 1 hasta el infinito de ((2i)! ^ 2 / (i! 2 ^ i) ^ 4 veces e ^ 21 / (2i-1))]

La cual puede parecer complicada, pero se expande así:

elipse perímetro aprox 2a pi [1 - (1/2) ^ 2 e ^ 2 - (1x3 / 2x4) ^ 2 e ^ 4/3 - (1x3x5 / 2x4x6) ^ 2 e ^ 6/5 - ...]

Los términos continúan infinitamente y, desafortunadamente, debemos calcular muchos términos para obtener una respuesta razonablemente cercana.

Serie infinita 2

Pero mi fórmula exacta favorita (porque da una respuesta muy cercana después de solo unos pocos términos) es la siguiente:

Primero calculamos "h":

h = (a − b)²(a + b)²

Luego usamos esta fórmula de "suma infinita":

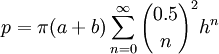
elipse perímetro aprox pi (a + b) sigma n = 0 a infinito de (0.5 elige n) ^ 2 h ^ n

(Nota: el es el Coeficiente Binomial con factoriales de medios enteros ... ¡Wow!)

Puede parecer un poco aterradora, pero se expande a esta serie de cálculos:

Cuantos más términos calculemos, más preciso será (el siguiente término es 25h⁴/16384, y cada vez se vuelve más pequeño, el siguiente es 49h⁵/65536, luego 441h⁶/1048576, etc.).

La fórmula perfecta

Hay una fórmula perfecta usando una integral:

p = 4a

π/2

√(1 − e² sin² θ) dθ

Pero calcularla necesita una cantidad infinita de términos ("Serie infinita 1" de arriba).

Comparar

Solo por diversión, calculé el perímetro usando las tres fórmulas de aproximación, y las dos fórmulas exactas (pero solo los primeros cuatro términos incluyendo el "1", por lo que siguen siendo solo una aproximación) para los siguientes valores de a y b:

	Círculo				Líneas

a:	10	10	10	10	10
b:	10	5	3	1	0
Aprox 1:	62.832	49.673	46.385	44.65	44.429
Aprox 2:	62.832	48.442	43.857	40.606	39.834
Aprox 3:	62.832	48.442	43.859	40.639	39.984
Serie 1:	62.832	48.876	45.174	43.204	42.951
Serie 2:	62.832	48.442	43.859	40.623	39.884
*Exacto:**	20π				40

*Exacto:

Cuando a=b, la elipse es un círculo y el perímetro es 2πa (62.832... en nuestro ejemplo).
Cuando b=0 (la forma son realmente dos líneas hacia adelante y hacia atrás) el perímetro es 4a (40 en nuestro ejemplo).

Todas obtienen correctamente el perímetro del círculo, pero solo Aprox 2 y 3 y la Serie 2 se acercan al valor de 40 para el caso extremo de b=0.

Calculadora de perímetro de elipse

Esta herramienta hace los cálculos de arriba, pero con más términos para cada serie.