Teorema del Binomio
Un binomio es un polinomio con dos términos
| ejemplo de un binomio |
¿Qué sucede cuando multiplicamos un binomio por sí mismo ... muchas veces?
Ejemplo: a+b
a+b es un binomio (los dos términos son a y b)
Multipliquemos a+b por sí mismo usando Multiplicación de Polinomios:
(a+b)(a+b) = a2 + 2ab + b2
Ahora usemos ese resultado y multipliquemos otra vez por a+b:
(a2 + 2ab + b2)(a+b) = a3 + 3a2b + 3ab2 + b3
Y otra vez:
(a3 + 3a2b + 3ab2 + b3)(a+b) = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Los cálculos se hacen cada vez más largos a medida que avanzamos,
pero hay algún tipo de patrón desarrollándose.
Ese patrón se resume en el Teorema del Binomio:
El Teorema del Binomio
No te preocupes ... ¡todo será explicado!
Y aprenderás muchos símbolos matemáticos geniales en el camino.
Exponentes
Primero, un resumen de los exponentes.
Un exponente dice cuántas veces usar algo en una multiplicación.
Ejemplo: 82 = 8 × 8 = 64
Un exponente de 1 significa que solo aparece una vez, para que obtengamos el valor original:
Ejemplo: 81 = 8
Un exponente de 0 significa no usarlo en absoluto, por lo que solo nos queda el número 1:
Ejemplo: 80 = 1
Exponentes de (a+b)
Ahora vamos con el binomio.
Usaremos el binomio más simple a+b, pero podríamos usar cualquier binomio.
Comencemos con el exponente 0 y construyamos hacia arriba.
Exponente 0
Cuando el exponente es 0, obtenemos 1:
(a+b)0 = 1
Exponente 1
Cuando el exponente es 0, obtenemos el valor original, sin modificaciones:
(a+b)1 = a+b
Exponente 2
El exponente 2 significa multiplicar por sí mismo (mira Cómo Multiplicar Polinomios):
(a+b)2 = (a+b)(a+b) = a2 + 2ab + b2
Exponente 3
Para el exponente 3 solo vuelve a multiplicar:
(a+b)3 = (a2 + 2ab + b2)(a+b) = a3 + 3a2b + 3ab2 + b3
Ahora tenemos suficiente para comenzar a hablar sobre el patrón.
El Patrón
En el último resultado obtuvimos:
a3 + 3a2b + 3ab2 + b3
Ahora, observa los exponentes de a. Empiezan en 3 y van disminuyendo: 3, 2, 1, 0:
De manera similar, los exponentes de b van en aumento: 0, 1, 2, 3:
Si numeramos los términos de 0 a n, obtenemos esto:
| k=0 | k=1 | k=2 | k=3 |
| a3 | a2 | a | 1 |
| 1 | b | b2 | b3 |
Lo que se puede juntar en esto:
an-kbk
¿Qué tal un ejemplo para ver cómo funciona?
Ejemplo: Cuando el exponente, n, es 3.
Los términos son:
| k=0: | k=1: | k=2: | k=3: |
|---|---|---|---|
| an-kbk = a3-0b0 = a3 |
an-kbk = a3-1b1 = a2b |
an-kbk = a3-2b2 = ab2 |
an-kbk = a3-3b3 = b3 |
¡Funciona como magia!
Coeficientes
Nos faltan los números (que se llaman coeficientes).
Veamos todos los resultados que obtuvimos antes, desde (a+b)0 hasta (a+b)3:
Y ahora mira solo los coeficientes (con un "1" donde no se escribió un coeficiente):
|
¡Esos números en realidad forman el Triángulo de Pascal! Cada número son solo los dos números que
|
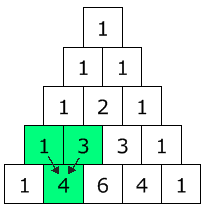 |
Armados con esta información, intentemos algo nuevo ... un exponente 4:
| para a los exponentes van 4,3,2,1,0: | a4 | + | a3 | + | a2 | + | a | + | 1 | ||
| para b los exponentes van 0,1,2,3,4: | a4 | + | a3b | + | a2b2 | + | ab3 | + | b4 | ||
| y los coeficientes van 1,4,6,4,1: | a4 | + | 4a3b | + | 6a2b2 | + | 4ab3 | + | b4 |
Y esa es la respuesta correcta (compárese con la parte superior de la página).
¡Lo hemos logrado!
Ahora podemos usar ese patrón para exponentes como 5, 6, 7, ... 50, ... 112, ... ¡lo que sea!
Ahora puedes tomarte un descanso.
Cuando regreses intenta calcular (a+b)5 por ti mismo.
Respuesta (pasa el cursor encima): a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Mediante una Fórmula
Nuestra siguiente tarea es escribirlo todo como una fórmula.Ya tenemos los exponentes resueltos:
an-kbk
Pero, ¿cómo escribimos una fórmula para "encuentra el coeficiente
del Triángulo de Pascal"...?
Bueno, ya existe una fórmula así:
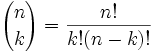
Comúnmente se conoce como "n en k" y representa de cuántas maneras diferentes podemos elegir k elementos de un conjunto de n elementos.
El "!" se lee como "factorial", por ejemplo 4! = 4×3×2×1 = 24
Puedes leer más en Combinaciones y Permutaciones.
|
Y coincide con el Triángulo de Pascal así: |
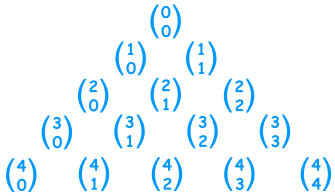 |
Ejemplo: Fila 4, término 2 en el Triángulo de Pascal es "6".
Veamos si la fórmula funciona:
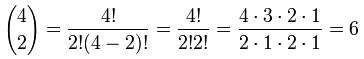
¡Sí, funciona! Prueba otro valor por ti mismo.
Poniéndolo todo junto
El último paso es poner todos los términos juntos en una
fórmula.
Pero estamos agregando muchos términos juntos ... ¿se puede hacer eso
usando una fórmula?
¡Sí! La práctica Notación Sigma nos
permite resumir tantos términos como queramos:
Notación Sigma
Ahora todo puede ir en una fórmula:
El Teorema del Binomio
Úsalo
OK ... no tendrá mucho sentido sin un ejemplo.Así que intentemos usarlo para n = 3:
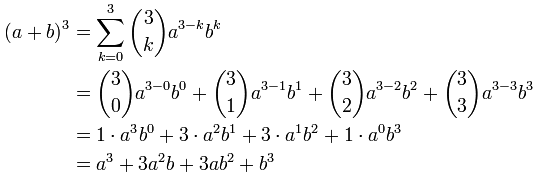
PERO ... generalmente es mucho más fácil recordar los patrones:
- Los exponentes del primer término comienzan en n y bajan
- Los exponentes del segundo término comienzan en 0 y suben
- Los coeficientes son del Triángulo de Pascal, o usando n!k!(n-k)!
Así:
Ejemplo: Desarrolla (y+5)4
| Empieza con los exponentes: | y450 | y351 | y252 | y153 | y054 |
| Incluye los coeficientes: | 1y450 | 4y351 | 6y252 | 4y153 | 1y054 |
Luego, escribe la respuesta (incluidos todos los cálculos, como 4×5, 6×52, etc.):
(y+5)4 = y4 + 20y3 + 150y2 + 500y + 625
También podemos querer calcular solo un término:
Ejemplo: ¿Cuál es el coeficiente de x3 en (2x+4)8 ?
Los exponentes de x3 son 8-5 (=3) para el "2x" y 5 para el "4":
(2x)345
(¿Por qué? He aquí el porqué:
| 2x: | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 4: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| (2x)840 | (2x)741 | (2x)642 | (2x)543 | (2x)444 | (2x)345 | (2x)246 | (2x)147 | (2x)048 |
Pero no necesitamos calcular todos los demás valores si solo queremos un término).
Y no olvidemos "8 en 5" ... podemos usar el Triángulo de Pascal, o calcular directamente:
n!k!(n-k)! = 8!5!(8-5)! = 8!5!3! = 8×7×63×2×1 = 56
Y obtenemos:
56(2x)345
Lo que se simplifica a:
458752 x3
Un coeficiente grande, ¿no?
Geometría
El Teorema del Binomio puede representarse de forma geométrica:
En 2 dimensiones, (a+b)2 = a2 + 2ab + b2
En 3 dimensiones, (a+b)3 = a3 + 3a2b + 3ab2 + b3
En 4 dimensiones, (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
(Lo siento, ¡no soy bueno dibujando en 4 dimensiones!)
Ejemplo Avanzado
Y un último, y sorprendente, ejemplo:
Ejemplo: Una fórmula para e (el Número de Euler)
Podemos usar el Teorema del Binomio para calcular e (el número de Euler).
e = 2.718281828459045... (los dígitos continúan para siempre sin repetir)
Se puede calcular usando:
(1 + 1/n)n
(Se vuelve más preciso cuanto mayor es el valor de n)
Esa fórmula es un binomio, ¿cierto? Así que usemos el Teorema del Binomio:
![(1 + 1/n)^n = Suma desde k=0 a n de [ (n en k) by 1^(n-k) por (1/n)^k ]](images/binomial-theorem-e.gif)
Primero, podemos quitar 1n-k ya que siempre es igual a 1:
![Sigma k=0 a n de [ (n en k) por (1/n)^k ]](images/binomial-theorem-e2.gif)
Y, mágicamente, la mayor parte de lo que queda se acerca a 1 a medida que n va al infinito:
De lo cual se sigue que:
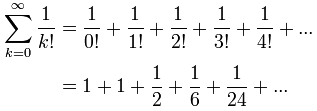
Con solo esos primeros términos obtenemos e ≈ 2.7083...
¡Intenta calcular más términos para una mejor aproximación! (Prueba la Calculadora Sigma)
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
Isaac Newton
Como nota, vale la pena mencionar que alrededor de 1665, Sir Isaac Newton ideó una versión "general" de la fórmula que no se limita a exponentes de 0, 1, 2 ... Espero escribir sobre eso algún día.
