Fracciones Parciales
Una forma de "romper" fracciones con polinomios en ellas.
¿Qué son las fracciones parciales?
Podemos hacer esto directamente:
Así:
... pero ¿cómo le hacemos para ir en la dirección opuesta?
Eso es lo que vamos a descubrir:
Cómo encontrar las "partes" que forman la
fracción simple
(las "fracciones parciales").
¿Por qué las queremos?
Antes que nada ... ¿por qué las queremos?
Porque las fracciones parciales son cada una más simples.
Esto puede ayudar a resolver la fracción más complicada. Por ejemplo, es muy útil en Cálculo Integral.
Descomposición en fracciones parciales
Déjame mostrarte cómo hacerlo.
El método se llama "Descomposición en fracciones parciales" y es así:
Paso 1: Factoriza lo de abajo
Paso 2: Escribe una fracción parcial para cada uno de esos factores
Paso 3: Multiplica todo por lo de abajo para que ya no tengamos fracciones
Paso 4: Ahora encuentra las constantes A1 y A2
Sustituir las raíces (los "ceros") de (x−2)(x+1) puede ayudar:
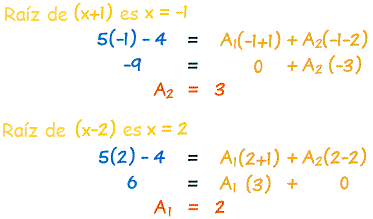
Y tenemos nuestra respuesta:
¡Eso fue fácil! ... casi demasiado fácil ...
... ¡porque puede ser mucho más difícil!
Ahora entraremos en detalles en cada paso.
Expresiones racionales propias
En primer lugar, esto solo funciona para Expresiones Racionales Propias, donde el grado de la parte superior es menor que la parte inferior.
El grado es el mayor exponente que tiene la variable.
- Propia: El grado de la parte superior es menor que el grado de la
parte inferior.
Propia: 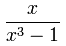xx3 − 1 el grado de arriba es 1
el grado de abajo es 3 - Impropia: El grado de la parte superior es mayor o igual que el
grado de la parte inferior.
Impropia: 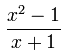x2 − 1x + 1 el grado de arriba es 2
el grado de abajo es 1
Si la expresión es impropia, entonces utiliza primero la división larga de polinomios.
Factorizando el denominador
Depende de ti factorizar el polinomio inferior. Lee Factorizando en Álgebra.
Pero no factorices utilizando números complejos ... es posible que debas detener algunos factores en cuadráticos (llamados cuadráticos irreducibles porque cualquier factorización adicional conduce a números complejos):
Ejemplo: (x2−4)(x2+4)
- x2−4 puede factorizarse en (x−2)(x+2)
- Pero x2+4 se factoriza en números complejos, así que no lo hagas
Así que lo mejor que podemos hacer es:
(x−2)(x+2)(x2+4)
- factores lineales
- factores cuadráticos irreducibles
B1x + C1(tu cuadrático)
Factores con exponentes
A veces puedes obtener un factor con un exponente, como (x−2)3 ...
Necesitas una fracción parcial para cada exponente de 1 en adelante.
Así:
Ejemplo:
1(x−2)3
Tiene como fracciones parciales:
A1x−2 + A2(x−2)2 + A3(x−2)3
Lo mismo puede ocurrir con las ecuaciones cuadráticas:
Ejemplo:
1(x2+2x+3)2
Tiene como fracciones parciales:
B1x + C1x2+2x+3 + B2x + C2(x2+2x+3)2
A veces, el uso de las raíces no lo resuelve
Incluso después de usar las raíces (ceros) del denominador, puedes terminar con constantes desconocidas.
Así que lo siguiente que debes hacer es:
Agrupar todas las potencias de x y luego resolverlo como un sistema de ecuaciones lineales.
¡Cielos! ¡Es mucho que procesar! Así que, vamos con un ejemplo para ayudarte a entenderlo:
Un gran ejemplo para unirlo todo
¡Aquí tienes un buen ejemplo completo para ti!
x2+15(x+3)2 (x2+3)
- Como (x+3)2 tiene un exponente de 2, necesita dos términos (A1 y A2).
- Y como (x2+3) es una cuadrática, necesitará Bx + C:
x2+15(x+3)2(x2+3) = A1x+3 + A2(x+3)2 + Bx + Cx2+3
Ahora multiplica todo por (x+3)2(x2+3):
x2+15 = (x+3)(x2+3)A1 + (x2+3)A2 + (x+3)2(Bx + C)
Hay un cero en x = −3 (porque x+3=0), así que probemos con eso:
(−3)2+15 = 0 + ((−3)2+3)A2 + 0
Y simplificamos a:
24 = 12A2
por lo tanto A2=2
Sustituyamos A2 por 2:
x2+15 = (x+3)(x2+3)A1 + 2x2+6 + (x+3)2(Bx + C)
Ahora desarrolla toda la expresión:
x2+15 = (x3+3x+3x2+9)A1 + 2x2+6 + (x3+6x2+9x)B + (x2+6x+9)C
Agrupa las potencias de x:
x2+15 = x3(A1+B)+x2(3A1+6B+C+2)+x(3A1+9B+6C)+(9A1+6+9C)
Separa las potencias y escríbelas como un Sistema de Ecuaciones Lineales:
| x3: | 0 | = | A1+B | |
| x2: | 1 | = | 3A1+6B+C+2 | |
| x: | 0 | = | 3A1+9B+6C | |
| Constantes: | 15 | = | 9A1+6+9C |
Simplifica y organiza ordenadamente:
| 0 | = | A1 | + | B | ||
| −1 | = | 3A1 | + | 6B | + | C |
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
Ahora, resuelve.
Puedes elegir tu propia forma de resolver esto... yo decidí restar la 4ª ecuación de la 2ª para empezar:
| 0 | = | A1 | + | B | ||
| −2 | = | 2A1 | + | 6B | ||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
Luego, resta 2 veces la 1ª ecuación de la 2ª:
| 0 | = | A1 | + | B | ||
| −2 | = | 4B | ||||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
Ahora sé que B = −(1/2).
¡Estamos llegando a alguna parte!
Y de la 1ª ecuación puedo deducir que A1 = +(1/2).
Y de la 4ª ecuación puedo deducir que C = +(1/2).
Resultado final:
Y ahora podemos escribir nuestras fracciones parciales:
x2+15(x+3)2(x2+3) = 12(x+3) + 2(x+3)2 + −x + 12(x2+3)
¡Uf! Mucho trabajo. Pero se puede lograr.
(Nota al margen: Me tomó casi
una hora hacer esto, porque tuve que
corregir 2 errores tontos en el camino).
Resumen
- Comienza con expresiones racionales propias (si no, haza la división primero)
- Factoriza lo de abajo en:
- factores lineales
- o factores cuadráticos "irreducibles"
- Escribe una fracción parcial para cada factor (y cada exponente de cada uno)
- Multiplica toda la ecuación por la parte inferior
- Encuentra los coeficientes a través de
- sustituir ceros del denominador
- hacer un sistema de ecuaciones lineales (de cada potencia) y resolviéndolo
- ¡Escribe tu respuesta!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
