Secciones Cónicas
Sección cónica: una sección (rebanada) a través de un cono.
 |
 |
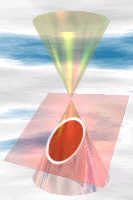 |
 |
 |
| Conos | Circunferencia | Elipse | Parábola | Hipérbola |
|---|---|---|---|---|
| corte recto a través | corte con poco ángulo | corte paralelo al borde del cono | corte con ángulo elevado |
¡Así que estas curvas están todas relacionadas!
¡Foco!
Las curvas también se pueden definir usando una línea recta y un
punto (llamadas directriz y foco).
Cuando medimos la distancia:
- desde el foco hasta un punto de la curva, y
- perpendicularmente desde la directriz hasta ese punto
las dos distancias siempre tendrán la misma proporción.
- Para una elipse, la proporción es menor que 1
- Para una parábola, la proporción es 1, por lo que las dos distancias son iguales.
- Para una hipérbola, la proporción es mayor que 1
La razón anterior se conoce como "excentricidad". Juega con esta animación:
Excentricidad
Podemos decir que cualquier sección cónica es:
"todos aquellos puntos cuya
distancia al foco es igual
a la excentricidad multiplicada por la distancia
a la directriz"
Para:
- 0 < excentricidad < 1 se tiene una elipse,
- excentricidad = 1 una parábola, y
- excentricidad > 1 una hipérbola.
Un círculo tiene una excentricidad igual a cero, por lo que la excentricidad nos muestra cuán "no circular" es la curva. Cuanto mayor es la excentricidad, menos curvada es.
Ejemplo: Las órbitas tienen una excentricidad menor que 1
Una excentricidad mayor que 1 no es realmente una órbita, ya que no regresa en un bucle, sino que simplemente pasa de largo.

Impresión artística de 'Oumuamua
Crédito: ESO/M. Kornmesser
El asteroide interestelar 'Oumuamua tiene una excentricidad de aproximadamente 1.2 en su trayectoria alrededor del Sol, lo que significa que no es parte de nuestro sistema solar:
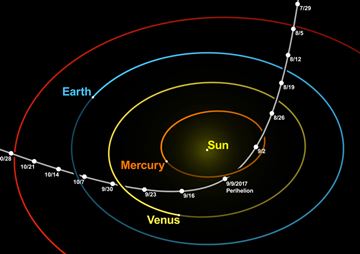
Crédito: Autores de Wikipedia nagualdesign y Tomruen
La órbita de la Tierra tiene una excentricidad de aproximadamente
0.0167 (casi un círculo).
La órbita de Marte tiene una excentricidad de aproximadamente 0.0934
(un poco menos circular).
Latus Rectum
No, no es ninguna grosería. El Latus Rectum hace referencia a la cuerda paralela a la directriz y que pasa por el foco. Su longitud:
- En una parábola, es igual a cuatro veces la longitud focal.
- En un círculo, es el diámetro.
- En una elipse, es 2b2/a (donde a y b son la mitad del diámetro mayor y menor).
Aquí está el eje mayor y el eje menor
de una elipse.
Hay un foco y una directriz a cada lado (es decir, un
par de ellos).
Ecuaciones
Cuando se coloca así en una gráfica x-y, la ecuación para una elipse es:
x2a2 + y2b2 = 1
El caso especial de un círculo (donde el radio=a=b):
x2a2 + y2a2 = 1
Y para una hipérbola es:
x2a2 − y2b2 = 1
Ecuación general
De hecho, podemos escribir una ecuación que vale para todas ellas.
Como son curvas planas (aunque salgan de cortar un sólido) sólo nos hacen falta coordenadas cartesianas "x" e "y".
Pero no son simples líneas rectas, así que no vale sólo con una "x" y una "y"... tenemos que ir al siguiente nivel, y usar- x2 y y2,
- y también x (sin ninguna y), y (sin ninguna x),
- x y y juntas (xy)
- y un término constante.
¡Ahí lo tienes!
También tendremos coeficientes (A,B,C etc.)
Así que la ecuación general que cubre todas las secciones cónicas es:
A partir de esta ecuación podemos crear ecuaciones para la circunferencia, elipse, parábola e hipérbola.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
