Prismas
Ve directamente a Área de la Superficie o Volumen.
- extremos idénticos
- caras planas
- ¡y la misma sección transversal a lo largo de toda su longitud!
Una sección transversal es la forma que se obtiene cuando se corta un objeto de manera recta.
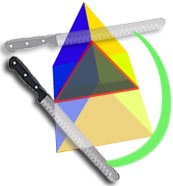
La sección de este objeto es un triángulo...
... tiene la misma sección en toda su longitud...
... así que es un prisma triangular.
|
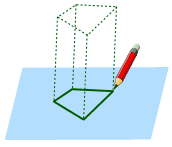
Intenta dibujar una forma en un trozo
de papel |
 |
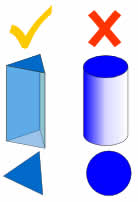
¡Sin curvas!
Un prisma es oficialmente un poliedro, así que todas las caras tienen que ser planas.
No hay lados curvos
Por ejemplo, un cilindro no es un prisma, porque tiene lados curvos.
Bases
Los extremos de un prisma son paralelos
y cada uno se llama base.
Lados
Las caras laterales de un prisma son paralelogramos
(Formas de 4 lados con lados opuestos paralelos)
Todos estos son prismas:
| Prisma cuadrado: | Sección: |
|
|
|
| Cubo: | Sección: |
| (sí, un cubo es un prisma, porque es un cuadrado en toda su longitud) (Mira también los prismas rectangulares) |
|
|
|
|
| Prisma triangular: | Sección: |
|
|
|
| Prisma pentagonal: | Sección: |
|
|
|
¡y más!

Example: Honeycomb
Bees store honey in hexagonal prisms.
The ends are hexagons and the 6 sides are rectangles.

Ejemplo: este cristal de hielo hexagonal.
Parece un hexágono, pero debido a que tiene cierto grosor, ¡en realidad es un prisma hexagonal!
Fotografía de la NASA / Alexey Kljatov.
Prismas regulares e irregulares
Todos los ejemplos anteriores son prismas regulares, porque la sección es regular (es decir, una forma con lados de la misma longitud).
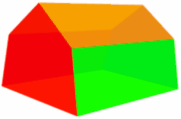
Aquí tienes un ejemplo de prisma irregular:
| Prisma irregular pentagonal: | ||
 |
 |
|
| Sección | ||
| (Es "irregular" porque el pentágono no tiene forma "regular"). |
||
Prisma recto vs oblicuo
Cuando los dos extremos están perfectamente alineados, es un prisma recto; de lo contrario, es un prisma oblicuo:
Área de la superficie de un prisma
+ Perímetro de la Base × Longitud
Ejemplo: ¿Cuál es el área de la superficie de un prisma donde el área de la base es de 25 m2, el perímetro de la base es de 24 m y la longitud es de 12 m?
(Nota: tenemos una Herramienta para ayudarte a calcular áreas).
Volumen de un prisma
El volumen de un prisma es simplemente el área de un extremo por la longitud del prisma
Volumen = Área de la Base × Longitud
Ejemplo: ¿Cuál es el volumen de un prisma cuyo extremo es 25 cm2 y que tiene 12 cm de longitud?
Juega aquí. La fórmula también funciona cuando se "inclina" (oblicua), pero recuerda que la altura forma un ángulo recto con la base:
Y esta es la razón:


La pila puede inclinarse, pero aún tiene el mismo volumen.
Más sobre las caras laterales
Las caras laterales de un prisma son paralelogramos (forma de 4 lados con lados opuestos paralelos).
Un prisma puede inclinarse hacia un lado, lo que lo convierte en un prisma oblicuo, pero los dos extremos siguen siendo paralelos y las caras laterales siguen siendo paralelogramos.
Pero si los dos extremos no son paralelos, no es un prisma.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
