Multiplicación de Números Complejos

Un Número Complejo es una combinación de un Número Real y un Número Imaginario:

Un Número Real es el tipo de número que usamos todos los días.

Ejemplos: 12.38, ½, 0, −2000

Un Número Imaginario, cuando lo elevamos al cuadrado da un resultado negativo:

un imaginario al cuadrado da negativo

La "unidad" imaginaria i al elevarla al cuadrado equivale a −1

i² = −1

Ejemplos: 5i, −3.6i, i/2, 500i

Un Número Complejo es una combinación de un Número Real y un Número Imaginario:

Ejemplos: 3.6 + 4i, −0.02 + 1.2i, 25 − 0.3i, 0 + 2i

Multiplicación

Para multiplicar números complejos:

Cada parte del primer número complejo

se multiplica por

cada parte del segundo número complejo

Aquí tienes una manera de acordarte de estas multiplicaciones. Usa "PIES", que significa "Primeros, Interiores, Exteriores, Segundos" (mira Multiplicación de Binomios para más detalles):

	Primeros: a × c Interiores: bi × c Exteriores: a × di Segundos: bi × di
(a+bi)(c+di) = ac + adi + bci + bdi²

De esta forma:

Ejemplo: (3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i

= 3 + 21i + 2i + 14i²

= 3 + 21i + 2i − 14 (porque i² = −1)

= −11 + 23i

Aquí hay otro ejemplo:

Ejemplo: (1 + i)²

(1 + i)²= (1 + i)(1 + i)

= 1×1 + 1×i + 1×i + i²

= 1 + 2i − 1 (porque i² = −1)

= 0 + 2i

¡Pero hay una manera más rápida!

Usa esta regla:

(a+bi)(c+di) = (ac−bd) + (ad+bc)i

Ejemplo:

(3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i

= −11 + 23i

¿Por qué funciona esa regla?

Es solo el método "PIES" después de un poco de trabajo:

(a+bi)(c+di)	=	ac + adi + bci + bdi²	método PIES
	=	ac + adi + bci − bd	(porque i²=−1)
	=	(ac − bd) + (ad + bc)i	(juntar términos similares)

Y ahí tienes el patrón (ac − bd) + (ad + bc)i.

Esta regla es ciertamente más rápida, pero si la olvidas, solo recuerde el método PIES.

Ahora veamos cómo se ve la multiplicación en el Plano Complejo.

El Plano Complejo

Éste es el plano complejo:

plano complejo

¡Es un plano para números complejos!

Podemos graficar un número complejo como 3 + 4i :

Se coloca:

3 unidades a lo largo (en el eje Real),
y 4 unidades arriba (en el eje Imaginario).

Multiplicar por i

Multipliquémoslo por i:

(3 + 4i) x i = 3i + 4i²

Y esto se simplifica (porque i² = −1):

−4 + 3i

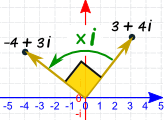Y aquí está lo bueno ... es lo mismo que girar en ángulo recto (90° o π/2)

¿Fue solo una extraña coincidencia?

Intentemos multiplicar por i nuevamente:

(−4 + 3i) x i = −4i + 3i² = −3 − 4i

y otra vez:

(−3 − 4i) x i = −3i − 4i² = 4 − 3i

y otra vez:

(4 − 3i) x i = 4i − 3i² = 3 + 4i

vector multiplicado por i 4 veces, resultando en una vuelta completa

Bueno, ¿no es asombroso? Cada vez que se gira noventa grados, hasta que termina donde comenzó.

Probémoslo en el número 1:

1 × i		= i
i × i		= −1
−1 × i		= −i
−i × i		= 1
¡Regresamos de nuevo al 1!

Cada vez una rotación en ángulo recto.

Elige tu propio número complejo y pruébalo por ti mismo, es una buena práctica.

Miremos más de cerca los ángulos ahora.

Forma Polar

Nuestro ya conocido número complejo 3 + 4i :

Aquí está de nuevo, pero

en forma polar:
(longitud y ángulo)

De modo que el número complejo 3 + 4i también puede escribirse mediante su longitud (5) y ángulo (0.927 radianes).

¿Cómo hacemos las conversiones?

Ejemplo: el número 3 + 4i

Podemos hacer una conversión de cartesianas a polares:

r = √(x² + y²) = √(3² + 4²) = √25 = 5
θ = tan^-1 (y/x) = tan^-1 (4/3) = 0.927 (a 3 decimales)

También podemos tomar coordenadas Polares y convertirlas en coordenadas Cartesianas:

x = r × cos( θ ) = 5 × cos( 0.927 ) = 5 × 0.6002... = 3 (suficientemente cerca)
y = r × sin( θ ) = 5 × sin( 0.927 ) = 5 × 0.7998... = 4 (suficientemente cerca)

De hecho, una forma común de escribir un número complejo en forma Polar es

x + iy	=	r cos θ + i r sin θ
	=	r(cos θ + i sin θ)

Y "cos θ + i sin θ" a menudo se escribe como "cis θ", así:

x + iy = r cis θ

cis es solo una abreviatura de cos θ + i sin θ

Entonces podemos escribir:

3 + 4i = 5 cis 0.927

En algunas materias, como la electrónica, ¡se usa mucho "cis"!

Vamos ahora con más multiplicaciones

Probemos con otra multiplicación:

Ejemplo: Multiplicar 1+i por 3+i

(1+i) (3+i) =1(3+i) + i(3+i)

=3 + i + 3i + i²

=3 + 4i − 1

=2 + 4i

Y aquí está el resultado en el Plano Complejo:

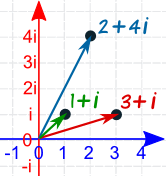
plano complejo 1+i, 3+i, 2+4i

Pero es más interesante ver esos números en Forma Polar:

Ejemplo: (continuación)

Convertir 1+i a Polar:

r = √(1² + 1²) = √2
θ = tan^-1 (1/1) = 0.785 (a 3 decimales)

Convertir 3+i a Polar:

r = √(3² + 1²) = √10
θ = tan^-1 (1/3) = 0.322 (a 3 decimales)

Convertir 2+4i a Polar:

r = √(2² + 4²) = √20
θ = tan^-1 (4/2) = 1.107 (a 3 decimales)

Echa un vistazo a los valores r por un minuto. ¿Están relacionados de alguna manera?
¿Y qué hay de los valores θ?

Aquí está esa multiplicación en un renglón (usando "cis"):

(√2 cis 0.785) × (√10 cis 0.322) = √20 cis 1.107

Esto es lo interesante:

√2 x √10 = √20
0.785 + 0.322 = 1.107

Entonces:

Las magnitudes se multiplican.
Y los ángulos se suman.

Al multiplicar en forma polar: multiplica las magnitudes, suma los ángulos.

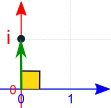
la i está en un ángulo de 90 grados en el plano complejo

Y es por eso que multiplicar por i gira por un ángulo recto:

i tiene magnitud 1 y forma un ángulo recto con el plano complejo.

Elevando al cuadrado

Para elevar al cuadrado un número complejo, multiplícalo por sí mismo:

multiplica las magnitudes: magnitud × magnitud = magnitud²
suma los ángulos: ángulo + ángulo = 2, entonces los duplicamos.

Resultado: elevar al cuadrado las magnitudes, duplicar el ángulo.

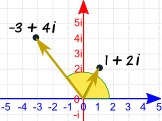
vector 1+2i al cuadrado es -3+4i

Ejemplo: Elevemos al cuadrado 1 + 2i:

(1 + 2i)(1 + 2i) = 1 + 4i + 4i² = −3 + 4i

En el diagrama, el ángulo parece estar (¡y está!) duplicado.

También:

La magnitud de (1+2i) = √(1² + 2²) = √5
La magnitud de (−3+4i) = √(3² + 4²) = √25 = 5

Así que la magnitud se elevó al cuadrado, también.

En general, un número complejo como:

r(cos θ + i sin θ)

Cuando se eleva al cuadrado resulta en:

r²(cos 2θ + i sin 2θ)

(la magnitud r se eleva al cuadrado y el ángulo θ se duplica.)

O en la notación más corta "cis":

(r cis θ)² = r² cis 2θ

De Moivre

Fórmula de De Moivre

Y el matemático Abraham de Moivre descubrió que funciona para cualquier exponente entero n:

[ r(cos θ + i sin θ) ]ⁿ = rⁿ(cos nθ + i sin nθ)

(la magnitud resulta ser rⁿ y el ángulo se convierte en nθ.)

O en la notación más corta "cis":

(r cis θ)ⁿ = rⁿ cis nθ

plano complejo 0-8i

Ejemplo: Calcula (1+i)⁶

Convierte 1+i a Polar:

r = √(1² + 1²) = √2
θ = tan^-1 (1/1) = π/4

En notación "cis": 1+i = √2 cis π/4

Ahora, con un exponente 6, r se vuelve r⁶, θ se hace 6θ:

(√2 cis π/4)⁶ = (√2)⁶ cis 6π/4 = 8 cis 3π/2

La magnitud es ahora 8, y el ángulo es 3π/2 (=270°)

O lo que es lo mismo 0−8i (mira el diagrama)

Resumen

Usa "PIES" para multiplicar números complejos,
O usa la fórmula:
(a+bi)(c+di) = (ac−bd) + (ad+bc)i
O usa la forma polar y luego multiplica las magnitudes y suma los ángulos.
La fórmula de De Moivre se puede usar para exponentes enteros:
[ r(cos θ + i sin θ) ]ⁿ = rⁿ(cos nθ + i sin nθ)
La forma polar r cos θ + i r sin θ a veces se abrevia como r cis θ

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).