Notación de conjuntos
Cómo describir un conjunto diciendo qué propiedades tienen sus miembros.
Pero también podemos "construir" un conjunto describiendo lo que hay en él.Aquí hay un ejemplo simple en notación de conjuntos:
Dice "el conjunto de todas las x, tal que la x es mayor que 0".
En otras palabras, cualquier valor mayor que 0
Notas:
- La "x" es sólo un marcador de posición, podría ser cualquier cosa, como { q | q > 0 }
- Algunas personas usan ":" en lugar de "|", así que escriben { x : x > 0 }
Tipo de número
También es normal mostrar que tipo de número es x, así:
- El símbolo
significa "un miembro de" (o simplemente "en")
- El símbolo
es el símbolo especial para los Números Reales.
Entonces queda así:
"el conjunto de todas las X que
son miembros de los Números Reales,
tales que x es mayor o igual a 3"
En otras palabras, "todos los números reales de 3 en adelante"
Hay otras formas en las que podríamos haber demostrado eso:
En la recta numérica se ve
así: 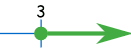
En notación de intervalos se ve así: [3, +∞)
Tipos de números
Vimos el símbolo (el símbolo especial de
los números reales). Aquí están los tipos
comunes de números:
 |
 |
 |
 |
 |
 |
| Números Naturales | Números Enteros | Números Racionales | Números Reales | Números Imaginarios | Números Complejos |
Ejemplo: { k 
| k >
5 }
"el conjunto de todas las k que son un miembro de los
Enteros, de tal manera que k es mayor que 5".
En otras palabras, todos los números enteros mayores de 5.
Esto también podría escribirse {6, 7, 8, ... } ...así que...:
{ k 
| k >
5 } = {6, 7, 8, ... }
¿Por qué usarla?
Cuando tenemos un conjunto simple como los números enteros de 2 a 6 podemos escribir:
{2, 3, 4, 5, 6}
Pero, ¿cómo podemos listar los números reales en el mismo intervalo?
{2, 2.1, 2.01, 2.001, 2.0001, ... ???
Así que en lugar de eso decimos cómo construir la lista:
{ x 
| x ≥ 2 y
x ≤ 6 }
Empieza con todos los números reales, luego limítalos entre
2 y 6 inclusivo.
También podemos usar la notación de conjuntos para hacer otras cosas, como esto:
{ x 
| x = x2
} = {0, 1}
Todos los números reales tales que x = x2
0 y 1 son los únicos casos en los que x = x2
Otro Ejemplo:
Ejemplo: x ≤ 2 o x > 3
La notación de conjuntos se ve así:
{ x
| x ≤ 2 o x >3 }
En la línea de números queda así:
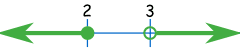
Usando la notación de Intervalos queda:
(−∞, 2] U (3, +∞)
Usamos una "U" para indicar Unión (unir dos conjuntos).
Definir un dominio
La notación de conjuntos es muy útil a la hora de definir dominios.
En su forma más simple, el dominio es el conjunto de todos los valores que entran en una función.
La función debe funcionar para todos los
valores que le demos, ¡así que depende de nosotros
asegurarnos de que el dominio sea correcto!
Ejemplo: El dominio de 1/x
1/x no está definida en x=0 (porque 1/0 es dividir entre cero).
Así que debemos excluir x=0 del Dominio:
El dominio de 1/x son todos los números reales, excepto el 0.
Podemos escribir esto así:
Dom(1/x) = {x
| x ≠ 0}
Ejemplo: El dominio de g(x)=1/(x−1)
1/(x−1) no está definida en x=1, por lo que debemos excluir x=1 del Dominio:
El dominio de 1/(x-1) son todos los números reales, excepto el 1
Usando la notación de conjuntos se escribe:
Dom( g(x) ) = { x | x ≠ 1}
Ejemplo: El dominio de √x
Son todos los números reales a partir de 0, porque no podemos tomar la raíz cuadrada de un número negativo (a menos que usemos Números Imaginarios, los cuales no estamos usando en este momento).
Se escribe:
Dom(√x) = {x
| x ≥ 0}
Ejemplo: El dominio de f(x) = x/(x2 − 1)
Para evitar la división por cero necesitamos: x2 − 1 ≠ 0
Factorizamos: x2 - 1 = (x−1)(x+1)
(x−1)(x+1) = 0 cuando x = 1 o x = −1, ¡lo cual queremos evitar!
Entonces:
Dom( f(x) ) = {x
| x ≠ 1,
x ≠ −1}
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
