Números Trascendentes
Número Trascendente
Un Número Trascendente es cualquier número que no es un número algebraico.
Ejemplos de números trascendentes incluyen π (Pi) y e (número de Euler).
Número Algebraico
¿Qué es entonces un Número Algebraico?
Dicho de forma sencilla, cuando tenemos una ecuación polinómica como (por ejemplo):
2x2 − 4x + 3 = 0
cuyos coeficientes (los números 2, −4 y 3) son racionales (números enteros o fracciones simples) ...
... entonces x es Algebraico.
(Lee Números algebraicos
para más detalles).
Podemos imaginar todo tipo de polinomios:
- x − 1 = 0 tiene x = 1,
- x + 1 = 0 tiene x = −1,
- 2x − 1 = 0 tiene x = ½,
- x2 − 2 = 0 tiene x = √2,
- y así sucesivamente
Todos los enteros, todos los números racionales y algunos números irracionales (como √2) son Algebraicos.
De hecho, es difícil pensar en un número que no sea Algebraico.
¡Pero existen! ¡Y muchísimos!

Trascienden el poder de los métodos algebraicos.
- Leonhard Euler
Números de Liouville
En 1844, Joseph Liouville propuso este número:
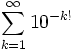 |
= 0.11000100000000000000000100…… |
| (el dígito es 1 si está en la posición k! después del decimal,
y 0 en caso contrario). |
Es un número muy interesante porque:
- es irracional, y
- no es la raíz de ninguna ecuación polinómica y, por lo tanto, no es algebraico.
De hecho, Joseph Liouville logró crear el primer Número Trascendente demostrable.
Ese número se conoce ahora como la Constante de Liouville y pertenece a la clase de los Números de Liouville.
Más Números Trascendentes
Hubo que esperar hasta 1873 para que se demostrara la trascendencia del primer número "no construido", cuando Charles Hermite demostró que e (el número de Euler) es trascendente.
Luego, en 1882, Ferdinand von Lindemann demostró que π (pi) es trascendente.
En realidad, demostrar que un número es Trascendente es bastante difícil, aunque se sabe que son muy comunes...
Los Números Trascendentes son Comunes
La mayoría de los números reales son trascendentes. El argumento para esto es:
- Los Números Algebraicos son "contables" (dicho de forma sencilla, la lista de los números enteros es "contable", y podemos organizar los números algebraicos de manera uno-a-uno con los números enteros, por lo que también son contables).
- Pero los números Reales son "No Contables".
- Y dado que un número Real es o bien Algebraico o bien Trascendente, los Trascendentes deben ser "No Contables".
- Por lo tanto, hay muchísimos más Trascendentes que Algebraicos.
El mismo argumento se aplica a los números complejos.
Función Trascendente
De la misma manera que un Número Trascendente "no es algebraico", una Función Trascendente también es "no algebraica".
De forma más formal, una función trascendente es una función que no puede ser construida en un número finito de pasos a partir de las funciones elementales y sus inversas.
Un ejemplo de Función Trascendente es la función seno sin(x).
Nota al pie: Más sobre los Números de LiouvilleUn Número de Liouville es un tipo especial de número trascendente que puede ser aproximado muy de cerca por números racionales. Más formalmente, un Número de Liouville es un número real x, con la propiedad de que, para cualquier entero positivo n, existen enteros p y q (con q > 1) tales que:
Ahora sabemos que x es irracional, por lo que siempre habrá una diferencia entre x y cualquier p/q: de ahí obtenemos la parte "0 <". Pero la segunda desigualdad nos muestra qué tan pequeña es esa diferencia. De hecho, la desigualdad dice que "el número puede ser aproximado infinitamente cerca, pero sin llegar nunca a él". Liouville logró demostrar que si un número tiene una serie de aproximaciones racionales que convergen rápidamente, entonces es trascendente. Otra propiedad interesante es que para cualquier entero positivo n, existe un número infinito de pares de enteros (p,q) que obedecen la desigualdad anterior. |
