Resolviendo Desigualdades
A veces necesitamos resolver desigualdades, como estas:
|
Símbolo
|
Significado
|
Ejemplo
|
||
|---|---|---|---|---|
|
>
|
mayor que
|
x + 3 > 2
|
||
|
<
|
menor que
|
7x < 28
|
||
|
≥
|
mayor o igual que
|
5 ≥ x − 1
|
||
|
≤
|
menor o igual que
|
2y + 1 ≤ 7
|
||
Resolver
Nuestra meta es tener a x (o cualquiera que sea la variable) separada a la izquierda del signo de desigualdad:
| Algo como: | x < 5 | |
| o: | y ≥ 11 |
Decimos que la desigualdad está "resuelta".
Ejemplo: x + 2 > 12
Resta 2 de ambos lados:
x + 2 − 2 > 12 − 2
Simplifica:
x > 10
¡Resuelto!
Cómo resolver
Resolver desigualdades es muy parecido a resolver ecuaciones ... hacemos la mayoría de las mismas cosas.
... pero también debemos prestar atención a la dirección de la desigualdad.
Dirección: hacia qué lado "señala" la flecha
¡Algunas cosas pueden cambiar la dirección!
< se convierte en >
> se convierte en <
≤ se convierte en ≥
≥ se convierte en ≤
Cosas que se pueden hacer
Estas cosas no afectan la dirección de la desigualdad:
- Sumar (o restar) un número de ambos lados
- Multiplicar (o dividir) ambos lados por un número positivo
- Simplificar un lado
Ejemplo: 3x < 7+3
Podemos simplificar 7 + 3 sin afectar la desigualdad:
3x < 10
Pero estas cosas cambian la dirección de la desigualdad ("<" se convierte en ">", por ejemplo):
- Multiplicar (o dividir) ambos lados por un número negativo
- Intercambiar los lados izquierdo y derecho
Ejemplo: 2y+7 < 12
Cuando intercambiamos los lados izquierdo y derecho, también debemos cambiar la dirección de la desigualdad:
12 > 2y+7
Aquí están los detalles:
Sumar o restar un valor
A menudo podemos resolver desigualdades sumando (o restando) un número de ambos lados (como en Introducción al Álgebra), de esta forma:
Ejemplo: x + 3 < 7
Si restamos 3 de ambos lados, obtenemos:
x + 3 − 3 < 7 − 3
x < 4
Y esa es nuestra solución: x < 4
En otras palabras, x puede ser cualquier valor menor que 4.
¿Qué hicimos?
|
Pasamos de esto: a esto: |
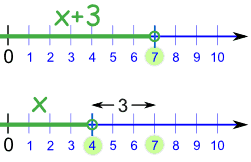 |
x+3 < 7 x < 4 |
||
Y eso funciona bien para sumar y restar, porque si sumamos (o restamos) la misma cantidad de ambos lados, no afecta la desigualdad
Ejemplo: Alex tiene más monedas que Brenda. Si tanto Alex como Brenda obtienen tres monedas más cada uno, Alex seguirá teniendo más monedas que Brenda.
¿Qué pasa si lo resuelvo, pero "x" está a la derecha?
No importa, simplemente cambia de lado, pero invierte el signo para que todavía "apunte" al valor correcto.
Ejemplo: 12 < x + 5
Si restamos 5 de ambos lados, obtenemos:
12 − 5 < x + 5 − 5
7 < x
¡Esa es una solución!
Pero es normal poner "x" en el lado izquierdo ...
... entonces volteemos los lados (¡y el signo de desigualdad!):
x > 7
¿Ves cómo el signo de desigualdad todavía "apunta" al valor más pequeño (7)?Y esa es nuestra solución: x > 7
Nota: "x" puede estar a la derecha, pero a la gente generalmente le gusta verla en el lado izquierdo.
Multiplicar o dividir por un valor
Otra cosa que hacemos es multiplicar o dividir ambos lados por un valor (como en Álgebra - Multiplicación).
Pero debemos ser un poco más cuidadosos (como verás).
Valores Positivos
Todo está bien si queremos multiplicar o dividir por un número positivo:
Ejemplo: 3y < 15
Si dividimos ambos lados entre 3 obtenemos:
3y/3 < 15/3
y < 5
Y esa es nuestra solución: y < 5
Valores Negativos
| Cuando multiplicamos o dividimos por un número
negativo debemos revertir la desigualdad. |
¿Por qué?
Bueno, solo mira la recta numérica.pero de −3 a −7 es una disminución.
¿Ves cómo se invierte el signo de desigualdad (de < a >)?
Probemos un ejemplo:
Ejemplo: −2y < −8
¡Dividamos ambos lados entre −2 ... e invierte la desigualdad!
−2y < −8
−2y/−2 > −8/−2
y > 4
Y esa es la solución correcta: y > 4
Entonces, solo recuerda:
Al multiplicar o dividir por un número negativo, revierte la desigualdad
Multiplicar o dividir por variables
Aquí hay otro ejemplo (¡capcioso!):
Ejemplo: bx < 3b
Parece fácil dividir ambos lados por b, lo que nos da:
x < 3
... pero espera ... si b es negativo necesitamos revertir la desigualdad así:
x > 3
Pero no sabemos si b es positivo o negativo, ¡así que no podemos responder este!
Para ayudarte a comprender, imagine reemplazar b con 1 o −1 en el ejemplo de bx < 3b:
- si b es 1, entonces la respuesta es x < 3
- pero si b es −1, entonces estaríamos resolviendo −x < −3, y la respuesta es x > 3
La respuesta podría ser x < 3 o x > 3 y no podemos elegir porque no conocemos b.
Por lo tanto:No intentes dividir por una variable para resolver una desigualdad (a menos que sepas que la variable siempre es positiva o siempre negativa).
Un ejemplo más grande
Ejemplo: x−32 < −5
Primero, quitemos el "/2" multiplicando ambos lados por 2.Debido a que estamos multiplicando por un número positivo, las desigualdades no cambiarán.
x−32 ×2 < −5 ×2
x−3 < −10
Ahora suma 3 a ambos lados:
x−3 + 3 < −10 + 3
x < −7
Y esa es nuestra solución: x < −7
¡Dos desigualdades a la vez!
¿Cómo resolvemos algo con dos desigualdades a la vez?
Ejemplo:
−2 < 6−2x3
< 4
Primero, removamos el "/3" multiplicando cada parte por 3.Debido a que estamos multiplicando por un número positivo, las desigualdades no cambian:
−6 < 6−2x < 12
Ahora resta 6 de cada parte:−12 < −2x < 6
Ahora divida cada parte entre 2 (un número positivo, de nuevo las desigualdades no cambian):
−6 < −x < 3
Ahora multiplique cada parte por −1. Debido a que estamos multiplicando por un número negativo, las desigualdades cambian de dirección.
6 > x > −3
¡Y esa es la solución!Pero para ser ordenado es mejor tener el número más pequeño a la izquierda, más grande a la derecha. Así que intercambiemos (y asegurémonos de que las desigualdades apuntan correctamente):
−3 < x < 6
Resumen
- Muchas desigualdades simples se pueden resolver sumando, restando, multiplicando o dividiendo ambos lados hasta que quede la variable por sí sola.
- Pero estas cosas cambiarán la dirección de la desigualdad:
- Multiplicar o dividir ambos lados por un número negativo
- Intercambiar los lados izquierdo y derecho.
- No multipliques ni dividas por una variable (a menos que sepas que siempre es positiva o siempre negativa).
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

